pressron

Table of Contents

II. Divine Machines

Celestial Mathematics

As we now skip ahead to focus mostly on Victorian England, some further context is required on the intellectual climate of the Victorian era. According to historian Daniel J. Cohen in his book Equations from God: Pure Mathematics and Victorian Faith, the observation of the planet Neptune in 1846 by Johann Gottfried Galle at the exact position it had been predicted to be by two mathematicians, Urbain Le Verrier and John Couch Adams, who had prognosticated its existence by observing the irregularities in the orbit of Uranus, prompted a great deal of excitement — a religious fervor, in fact — about pure mathematics in Europe and America, seeing mathematics as no less than a supreme form of religious worship:

⊕Equations From God, pp. 3-6 At work the mathematician becomes a pure spirit, rising out of the confinement of his material body… He has no use for everyday faculties like sight, but rather operates with a higher, far more powerful internal sense. This mathematical faculty is not a passive receptor of information, but is instead a penetrating instrument that attains the grandest truths, all of which lie beyond the reach of our five bodily senses.

⊕
Planet Neptune (source: Wikipedia, NASA).

In the first published book on Neptune, J. P. Nichol, a professor of astronomy at the University of Glasgow, portrayed the discovery in a similarly dramatic way while portraying the mind of the mathematician as in touch with the underlying properties of the universe.

… The discovery of Neptune was for J. P. Nichol and his contemporaries an “ever-memorable adventure into that region of pure thought,” a transcendent journey into the land of the fundamental ideas of our universe. Praising the ideal nature of the language of mathematics, Nichol highlighted the fact that Le Verrier and Adams had the allure of pure mathematics in the victorian age used “the symbols and processes of our most recondite Analysis,” which alone can access invisible, eternal laws. Such sentiments were obviously more than paeans to mathematics; they were strong professions of a peculiar kind of Victorian faith. As the British astronomer and mathematician Mary Somerville recalled in her autobiography, “Nothing has afforded me so convincing a proof of the unity of the Deity as these purely mental conceptions of numerical and mathematical science which have been by slow degrees vouchsafed to man . . . all of which must have existed in that sublimely omniscient Mind from eternity.” Somerville thought herself extremely lucky to have had a career that dealt daily with the divine forms of pure mathematics.

… With such intense religious meaning attached to the mathematical prognostication of Neptune, the discipline of mathematics quickly became fodder for sermons. In an 1848 oration, the American Congregational minister Horace Bushnell declared that mathematics clearly consisted of “those pure and incorruptible formulas which already were before the world was, that will be after it, governing throughout all time and space, being, as it were, as integral part of God.” The symbols and correspondences of mathematics thus “put the mathematician in profound communion with the Divine Thought.” Although he was not a mathematician, the religious idealism of his scientific brethren was encouraging to Bushnell. Revelations from the divine sphere comprise the epiphanic moments of science, he believed, as mankind communes with God’s great mathematical laws and concepts. “Geometrical and mathematical truths become the prime sources of scientific inspiration; for these are the pure intellectualities of all created being,” Bushnell proclaimed. At times of discovery the scientist is “raised to a pitch of insight and becomes a seer, entering into things through God’s constitutive ideas, to read them as from God.”

In an 1850s sermon, the Oxford clergyman Adam S. Farrar also diverged from his normal subject matter to inform his audience of the profound significance of pure mathematics. “If any branch of knowledge appeared eminently unlikely to unfold to us any information about God, you would think it would be that system of symbolic formulæ and abstract notions,” he noted, “And yet when we apply it to predict the attractions of the heavenly bodies in periods yet to come, it unfolds to us some results of extraordinary grandeur.” Farrar therefore concluded that the equations of mathematics ultimately “reveal to us the infinite wisdom of God.” “Who can contemplate these amazing results, which manifest the infinite contrivance of the Almighty Architect, without a feeling of devout thankfulness that we have been permitted thus to discover traces of the high and lofty One who inhabiteth eternity!” he declared.

Edward Everett, the New England politician, Harvard administrator, and orator, summarized the feelings of many early Victorian clergymen and mathematicians alike in an 1857 lecture at the inauguration of Washington University in St. Louis. He eloquently announced to the spectators, “In the pure mathematics we contemplate absolute truths, which existed in the Divine Mind before the morning stars sang together, and which will continue to exist there, when the last of their radiant host shall have fallen from heaven.” Much of Everett’s audience surely nodded in agreement with his lofty assessment of mathematics.

This commingling of the mathematical with the spiritual was not exactly new. Western thought had long given the discipline a lofty spot in the pantheon of knowledge. Indeed, since the height of ancient Greece philosophers have often considered mathematics so sublime that it transcends the profane realm of humanity and ascends into the pure realm of the divine.

We’ve seen a similar religious sentiment expressed by Leibniz, but it may be surprising to learn that similar religious motivations underlied mathematics in the nineteenth century, as well. It is not entirely surprising, then, that a miraculous view of mathematics persists to this day (see the Preface).

The first theoretical breakthrough we will visit is found in an 1830 book by the English mathematician George Peacock (1791-1858), A Treatise on Algebra, which may be considered as the foundational work of modern abstract algebra, meaning the study of mathematical structures by examining the relationships between “abstract” objects represented by symbols, rather than considering the symbols as placeholders for arbitrary concrete numbers. Peacock writes:

⊕A Treatise on Algebra, pp. vi-xxi Algebra has always been considered as merely such a modification of Arithmetic as arose from the use of symbolical language, and the operations of one science have been transferred to the other without any statement of an extension of their meaning and application: thus symbols are assumed to be the general and unlimited representatives of every species of quantity: the operations of Addition and Subtraction in their simple arithmetical sense, are assumed to be denoted by the signs + and – , and to be used in connecting such symbols with each other: Multiplication and Division, two inverse operations in Arithmetic, are supposed to be equally applicable to all quantities which symbols may denote, without any necessary modification of their meaning… [T]he consequences of those operations, and of the assumptions connected with them, must be determined by the fundamental rules for performing them, which are independent of each other, or whose necessary connection is dependent upon their assumed universalities only: and the imposition of the names Addition and Subtraction upon such operations, and even their immediate derivation from a science in which their meaning and applications are perfectly understood and strictly limited, can exercise no influence upon the results of a science, which regards the combination of signs and symbols only, according to determinate laws, which are altogether independent of the specific values of the symbols themselves.

⊕
The clock tower at Trinity College, Cambridge, George Peacock and Charles Babbage’s alma mater (Source: Wikipedia)

It is this immediate derivation of Algebra from Arithmetic, and the close connection which it has been attempted to preserve between those sciences, which has led to the formation of the opinion, that one is really founded upon the other… it would appear … that such an opinion would cease to be maintainable…

… It is the admission of this principle, in whatever manner we are led to it, which makes it necessary to consider symbols not merely as the general representatives of numbers, but of every species of quantity, and likewise to give a form to the definitions of the operations of Algebra, which must render them independent of any subordinate science: for in the first place the symbols, whatever they denote, must be unlimited in value, and it is only by their ceasing to be abstract numbers that we shall be enabled to interpret the affections which the signs + or – (or any other signs) essentially attached to them may be supposed to express: and in the second place, in framing the definitions of algebraical operations, to which symbols thus afiected are subjected, we must necessarily omit every condition which is in any way connected with their specific value or representation: in other words, the definitions of those operations must regard the laws of their combination only. thus the operations denoted by + and – must regard the affection of symbols … by them, according to an assumed law for the concurrence of those signs…

If we should rest satisfied with such assumed rules for the combinations of symbols and of signs by such operations, which are perfectly independent of any interpretation of their meaning, or of their relation to each other, we should retain in the results obtained all the symbols which were incorporated, without possessing the power of any further simplification: it is as a first step to effect such further reduction of the results, and in order to define the symbolical relation of pairs of those operations to each other, that we assume the operation denoted by $+$ to be the inverse of that which is denoted by $-$ , and conversely; and the operation denoted by $\times$ to be the inverse of that which is denoted by $\div$, or conversely: or, in other words, we consider $a + b - b$ and $a - b + b$ , $a \times b \div b$ or $\frac{ab}{b}$ to be identical in signification with the simple symbol $a$.

Under such a form, the fundamental operations of Algebra are altogether symbolical, and we might proceed to deduce symbolical results and equivalent forms by terms of them without any regard to the principles of any other science; and it would merely require the introduction of some such sign as = in the place of the words algebraical result of, or algebraically equivalent to, to connect the results obtained with the symbolical representation of the operations which produce them, in order to supersede altogether the use of ordinary language.

It is at this point that the essential connexion of Algebra and Arithmetic may properly be said to commence: for a science of mere signs and symbols must terminate in the consequences of their laws of combination, unless they can be associated by interpretation, with real operations upon real magnitudes with specific representations.

… One of the most important consequences of this view of the principles and operations of Algebra, is the complete separation which it effects of the laws for the combination of symbols from the principles of their interpretation: common systems of Algebra, the previous interpretation assumed or understood, of the operations of Algebra, determines, or is supposed to determine, the results which are obtained, and the laws of symbolical combinations: but the case is reversed in the system which I have ventured to propose, where the laws of symbolical combinations are assumed, not arbitrarily, but with a general reference to their anticipated interpretation in the subordinate science of arithmetic… it being kept in mind however, that such interpretations are never mathematically necessary in any single case, though the connection of the interpretations of a series of dependent results may become so: or, in other words, the admitted interpretation of any one of them upon which the others depend may impose a mathematical necessity upon all the others in the series, but not conversely.

It is by means of such interpretations, and the principles which limit and govern them, that Algebra becomes accommodated to the form and peculiar character of every subordinate science: to Arithmetic in the first instance, as the general science of suggestion: to Geometry, as defining the relations of lines to each other, with respect to magnitude and position: to Mechanics and Dynamics, as defining forces, their directions and effects, whether to produce rest or motion: and similarly to every other branch of natural philosophy, which can be made to depend, by approximation, at least, upon fixed and invariable principles…

⊕A Treatise on Algebra, p. 1 CHAP. I.

1. Algebra may be defined to be, the science of general reasoning by symbolical language. … it has been termed Universal Arithmetic; but this definition is defective, inasmuch as it assigns for the general object of the science, what can only be considered as one of its applications.
2. The symbols of Algebra may be made the representatives of every species of quantity, whether abstract or concrete : the operations to which they are subject are perfectly general, and are in no respect affected by the nature of the quantities which the symbols denote, being determined solely by the definitions and assumptions which constitute the first principles of the science.

This clear treatment of the transition of algebra from a mere “modification of arithmetic” to an abstract science stands for itself. Peacock speaks of interpretations — the assignment of concrete meaning to the symbols — that connect algebra with arithmetic, but the idea of abstract algebra has taken such a hold in mathematics, that today, one hardly thinks of an algebraic structure as having different “interpretations”; instead, there are just instances or examples of it, and we are satisfied that the “science of mere signs and symbols must terminate in the consequences of their laws of combination.”

The mathematical historian John Michael Dubbey claims that the totality of Peacock’s treatment had actually been present in a series of unpublished manuscripts written in 1821 by his friend and co-founder of Cambridge’s Analytical Society,Whose aim — at which it was highly successful — was to promote the use of the Leibinizian notation of differentiation (as a fraction of total or partial differentials) over the Newtonian dot notation, which had been prevalent in England. Charles Babbage:Babbage, Peacock and Modern Algebra, pp. 301-302 “While including all of Peacock’s ideas on the subject, Babbage’s exposition is actually superior… We have now established a quite remarkable similarity in the thinking of two contemporary mathematicians, and we have the evidence of Peacock’s letter that he had read Babbage’s work nine years prior to his own publication. However, there is not a shred of additional evidence to support a charge of plagiarism. … In view of such lack of evidence it seems idle to put forward any theory to account for the astonishing similarity of Babbage’s unpublished and Peacock’s published work. It might even be possible that Peacock took in Babbage’s ideas unconsciously and with full integrity turned them out as his own a few years later. In any case, Babbage was too busy working on his computer and reforming British science generally to worry very much about the priority of any of his inventions in pure mathematics. Sufficient to say that in the discovery of so called ‘modern algebra’, Babbage’s work in 1821 was substantial.”

Babbage wasEquations From God, p. 153 “possibly the best-known academic mathematician who spoke his mind on theological issues… Babbage’s Ninth Bridgewater Treatise (1837) brazenly employed mathematical principles to support religious doctrine. For instance, he used equations from Laplace’s Théorie Analytique des Probabilités and Poisson’s Recherches sur la Probabilité des Jugements to counter David Hume’s repudiation of miracles, calculating the probability that so many witnesses could have been mistaken about seeing Jesus rise from the dead.”

Motion of the Hand, Office of the Mind

Indeed, by the 1830s, Charles Babbage (1791-1871) was preoccupied by matters other than pure mathematics. His most famous work, more than a product of the religious and academic climate of the era, was a product of the technological climate. The industrial revolution in England, with its ingenious machines like the Jacquard Loom, inspired Babbage to use the new technology of automation for the automation of intellectual labor. In 1834, Dionysius Lardner (1793-1859), an Irish science writer, wrote an impassioned report about an invention he had witnessed — a machine that can produce numerical calculation tables — and found to be a revolutionary achievement that, sadly, in his opinion, had not won the attention and funding it deserved:

⊕Babbage’s Calculating Engine By Dr. Dionysius Lardner From the Edinburgh Review, July, 1834, No. CXX, in Morrison, Charles Babbage and his Calculating Engines pp. 164-166 There is no position in society more enviable than that of the few who unite a moderate independence with high intellectual qualities. Liberated from the necessity of seeking their support by a profession, they are unfettered by its restraints, and are enabled to direct the powers of their minds, and to concentrate their intellectual energies on those objects exclusively to which they feel that their powers may be applied with the greatest advantage to the community, and with the most lasting reputation to themselves. On the other hand, their middle station and limited income rescue them from those allurements to frivolity and dissipation, to which rank and wealth ever expose their possessors. ⊕
Other professors appointed to the Lucasian Chair include Isaac Newton, Paul Dirac, Stephen Hawking, and, in the final episode of Star Trek: The Next Generation, Lieutenant Commander Data.Placed in such favourable circumstances, Mr. Babbage selected science as the field of his ambition; and his mathematical researches have conferred on him a high reputation, wherever the exact sciences are studied and appreciated. The suffrages of the mathematical world have been ratified in his own country, where he has been elected to the Lucasian Professorship in his own University—a chair, which, though of inconsiderable emolument, is one on which Newton has conferred everlasting celebrity. But it has been the fortune of this mathematician to surround himself with fame of another and more popular kind, and which rarely falls to the lot of those who devote their lives to the cultivation of the abstract sciences. This distinction he owes to the announcement, some years since, of his celebrated project of a Calculating Engine. A proposition to reduce arithmetic to the dominion of mechanism—to substitute an automaton for a compositor—to throw the powers of thought into wheel-work could not fail to awaken the attention of the world. To bring the practicability of such a project within the compass of popular belief was not easy: to do so by bringing it within the compass of popular comprehension was not possible. It transcended the imagination of the public in general to conceive its possibility; and the sentiments of wonder with which it was received, were only prevented from merging into those of incredulity, by the faith reposed in the high attainments of its projector. This extraordinary undertaking was, however, viewed in a very different light by the small section of the community, who, being sufficiently versed in mathematics, were acquainted with the principle upon which it was founded. By reference to that principle, they perceived at a glance the practicability of the project; and being enabled by the nature of their attainments and pursuits to appreciate the immeasurable importance of its results, they regarded the invention with a proportionately profound interest.

… There are, nevertheless, many persons who, admitting the great ingenuity of the contrivance, have, notwithstanding, been accustomed to regard it more in the light of a philosophical curiosity, than an instrument for purposes practically useful. This mistake (than which it is not possible to imagine a greater) has arisen mainly from the ignorance which prevails of the extensive utility of those numerical tables which it is the purpose of the engine in question to produce. There are also some persons who, not considering the time requisite to bring any invention of this magnitude to perfection in all its details, incline to consider the delays which have taken place in its progress as presumptions against its practicability. These persons should, however, before they arrive at such a conclusion, reflect upon the time which was necessary to bring to perfection engines infinitely inferior in complexity and mechanical difficulty. Let them remember that—not to mention the invention of that machine-the improvements alone introduced into the steam-engine by the celebrated Watt, occupied a period of not less than twenty years of the life of that distinguished person, and involved an expenditure of capital amounting to £50,000. The calculating machinery is a contrivance new even in its details. Its inventor did not take it up already imperfectly formed, after having received the contributions of human ingenuity exercised upon it for a century or more. It has not, like almost all other great mechanical inventions, been gradually advanced to its present state through a series of failures, through difficulties encountered and overcome by a succession of projectors. It is not an object on which the light of various minds has thus been shed. It is, on the contrary, the production of solitary and individual thought—begun, advanced through each successive stage of improvement, and brought to perfection by one mind. Yet this creation of genius, from its first rude conception to its present state, has cost little more than half the time, and not one-third of the expense, consumed in bringing the steam-engine (previously far advanced in the course of improvement) to that state of comparative perfection in which it was left by Watt. Short as the period of time has been which the inventor has devoted to this enterprise, it has, nevertheless, been demonstrated, to the satisfaction of many scientific men of the first eminence, that the design in all its details, reduced, as it is, to a system of mechanical drawings, is complete; and requires only to be constructed in conformity with those plans, to realize all that its inventor has promised.

⊕pp. 214-219 … This application of an almost metaphysical system of abstract signs, by which the motion of the hand performs the office of the mind, and of profound practical skill in mechanics alternately, to the construction of a most complicated engine, forcibly reminds us of a parallel in another science, where the chemist with difficulty succeeds in dissolving a refractory mineral, by the alternate action of the most powerful acids, and the most caustic alkalies, repeated in long-continued succession.

⊕
Children enjoying the techonological advances of the industrial revolution working the looms at a cotton mill. An 1840 engraving from The Life and Adventures of Michael Armstrong, the Factory Boy by Frances Milton Trollope (source: The British Library).

This important discovery was explained by Mr. Babbage, in a short paper read before the Royal Society, and published in the Philosophical Transactions in 1826. It is to us more a matter of regret than surprise, that the subject did not receive from scientific men in this country that attention to which its importance in every practical point of view so fully entitled it. To appreciate it would indeed have been scarcely possible, from the very brief memoir which its inventor presented, unaccompanied by any observations or arguments of a nature to force it upon the attention of minds unprepared for it by the nature of their studies or occupations. In this country, science has been generally separated from practical mechanics by a wide chasm. It will be easily admitted, that an assembly of eminent naturalists and physicians, with a sprinkling of astronomers, and one or two abstract mathematicians, were not precisely the persons best qualified to appreciate such an instrument of mechanical investigation as we have here described. We shall not therefore be understood as intending the slightest disrespect for these distinguished persons, when we express our regret, that a discovery of such paramount practical value, in a country pre-eminently conspicuous for the results of its machinery, should fall still-born and inconsequential through their hands, and be buried unhonoured and undiscriminated in their miscellaneous transactions. We trust that a more auspicious period is at hand; that the chasm which has separated practical from scientific men will speedily close; and that that combination of knowledge will be effected, which can only be obtained when we see the men of science more frequently extending their observant eye over the wonders of our factories, and our great practical manufacturers, with a reciprocal ambition, presenting themselves as active and useful members of our scientific associations. When this has taken place, an order of scientific men will spring up, which will render impossible an oversight so little creditable to the country as that which has been committed respecting the mechanical notation. This notation has recently undergone very considerable extension and improvement. An additional section has been introduced in to it; designed to express the process of circulation in machines, through which fluids, whether liquid or gaseous, are moved. Mr. Babbage, with the assistance of a friend, who happened to be conversant with the structure and operation of the steam-engine, has illustrated it with singular felicity and success in its application to that machine. An eminent French surgeon, on seeing the scheme of notation thus applied, immediately suggested the advantages which must attend it as an instrument for expressing the structure, operation, and circulation of the animal system; and we entertain no doubt of its adequacy for that purpose. Not only the mechanical connection of the solid members of the bodies of men and animals, but likewise the structure and operation of the softer parts, including the muscles, integuments, membranes, &c.; the nature, motion, and circulation of the various fluids, their reciprocal effects, the changes through which they pass, the deposits which they leave in various parts of the system; the functions of respiration, digestion, and assimilation-all would find appropriate symbols and representatives in the notation, even as it now stands, without those additions of which, however, it is easily susceptible. Indeed, when we reflect for what a very different purpose this scheme of symbols was contrived, we cannot refrain from expressing our wonder that it should seem, in all respects, as if it had been designed expressly for the purposes of anatomy and physiology.

Another of the uses which the slightest attention to the details of this notation irresistibly forces upon our notice, is to exhibit, in the form of a connected plan or map, the organization of an extensive factory, or any great public institution, in which a vast number of individuals are employed, and their duties regulated (as they generally are or ought to be) by a consistent and well-digested system. The mechanical notation is admirably adapted, not only to express such an organized connection of human agents, but even to suggest the improvements of which such organization is susceptible-to betray its weak and defective points, and to disclose, at a glance, the origin of any fault which may, from time to time, be observed in the working of the system. Our limits, however, preclude us from pursuing this interesting topic to the extent which its importance would justify. We shall be satisfied if the hints here thrown out should direct to the subject the attention of those who, being most interested in such an inquiry, are likely to prosecute it with greatest success.

… The idea of calculation by mechanism is not new. Arithmetical instruments, such as the calculating boards of the ancients, on which they made their computations by the aid of counters-the Abacus, an instrument for computing by the aid of balls sliding upon parallel rods-the method of calculation invented by Baron Napier, called by him Rhabdology, and since called Napier’s bones-the Swan Pan of the Chinese-and other similar contrivances, among which more particularly may be mentioned the Sliding Rule, of so much use in practical calculations to modern engineers, will occur to every reader: these may more properly be called arithmetical instruments, partaking more or less of a mechanical character. But the earliest piece of mechanism to which the name of “calculating machine” can fairly be given, appears to have been a machine invented by the celebrated Pascal. This philosopher and mathematician, at a very early age, being engaged with his father, who held an official situation in Upper Normandy, the duties of which required frequent numerical calculations, contrived a piece of mechanism to facilitate the performance of them.

… This mechanism, which was invented about the year 1650, does not appear to have been brought into any practical use; and seems to have speedily found its appropriate place in a museum of curiosities. It was capable of performing only particular arithmetical operations, and these subject to all the chances of error in manipulation; attended also with little more expedition (if so much), as would be attained by the pen of an expert computer.

… [O]ne of the most remarkable attempts of this kind which has been made since that of Pascal, was a machine invented by Leibnitz, of which we are not aware that any detailed or intelligible description was ever published. Leibnitz described its mode of operation, and its results, in the “Berlin Miscellany,” but he appears to have declined any description of its details… He goes on to say that the process of division is performed independently of a succession of subtractions, such as that used by Pascal.

It appears that this machine was one of an extremely complicated nature, which would be attended with considerable expense of construction, and only fit to be used in cases where numerous and expensive calculations were necessary… Nevertheless, it does not appear that this contrivance, of which the inventor states that he caused two models to be made, was ever applied to any useful purpose; nor indeed do the mechanical details of the invention appear ever to have been published.

Even had the mechanism of these machines performed all which their inventors expected from them, they would have been still altogether inapplicable for the purposes to which it is proposed that the calculating machinery of Mr. Babbage shall be applied. They were all constructed with a view to perform particular arithmetical operations, and in all of them the accuracy of the result depended more or less upon manipulation. The principle of the calculating machinery of Mr. Babbage is perfectly general in its nature, not depending on any particular arithmetical operation, and is equally applicable to numerical tables of every kind.

Note the similarities between Lardner’s vision of automatic computation and that of Leibniz, two centuries prior, as both discuss the possibility of expressing and simulating both man-made and natural systems. Also of note is Lardner’s philosophical observation, “the motion of the hand performs the office of the mind”, pointed out by Leibniz in his discussion of blind thought, and which later served as the very core of Turing’s seminal philosophical treatment of the theory of computation.

More amusing are Lardner’s observations of the accidental and systemic difficulties standing in the way of the dream of what can only be called computing, from Babbage’s technical salesmanship, “unaccompanied by any observations or arguments of a nature to force it upon the attention of minds unprepared for it by the nature of their studies or occupations,” — we will shortly see exactly what he means — to the social status of practical technological progress compared with that of science, from which it is “separated … by a wide chasm.” Lardner hopes for an age when “the chasm which has separated practical from scientific men will speedily close; and that that combination of knowledge will be effected, which can only be obtained when we see the men of science more frequently extending their observant eye over the wonders of our factories, and our great practical manufacturers, with a reciprocal ambition, presenting themselves as active and useful members of our scientific associations.”

Charles Babbage wrote of the invention of that miraculous machine:

⊕Passages from the Life of a Philospher, p. 42 The earliest idea that I can trace in my own mind of calculating arithmetical Tables by machinery arose in this manner :—

One evening I was sitting in the rooms of the Analytical Society, at Cambridge, my head leaning forward on the Table in a kind of dreamy mood, with a Table of logarithms lying open before me. Another member, coming into the room, and seeing me half asleep, called out, “Well, Babbage, what are you dreaming about?” to which I replied, “I am thinking that all these Tables (pointing to the logarithms) might be calculated by machinery.” … The event must have happened either in 1812 or 1813.

He wrote:

⊕Charles Babbage, Calculating Engines, 1889, in Morrison, Charles Babbage and his Calculating Engines p. 322 It is not a bad definition of man to describe him as a tool-making animal. His earliest contrivances to support uncivilized life, were tools of the simplest and rudest construction. His latest achievements in the substitution of machinery, not merely for the skill of the human hand, but for the relief of the human intellect, are founded on the use of tools of a still higher order.

The following text by Babbage about his greatest invention, the Analytical Engine, designed to be capable of symbolic algebraic computations in addition to numerical ones, demonstrates the difficulty in assessing Babbage’s theoretical contribution to the field of computation, and explains why his treatment of the subject was probably unknown to — and certainly ignored by — those twentieth century scholars who studied the subject of computation. While certainly entertaining, the text is a curious blend of philosophical, theoretical, practical and business considerations:

⊕Passages from the Life of a Philospher, pp. 465-471 A considerable time after the translation of Menabrea’s memoir had been published, and after I had made many drawings of the Analytical Engine and all its parts, I began to meditate upon the intellectual means by which I had reached to such advanced and even to such unexpected results. I reviewed in my mind the various principles which I had touched upon in my published and unpublished papers, and dwelt with satisfaction upon the power which I possessed over mechanism through the aid of the Mechanical Notation. I felt, however, that it would be more satisfactory to the minds of others, and even in some measure to my own, that I should try the power of such principles as I had laid down, by assuming some question of an entirely new kind, and endeavouring to solve it by the aid of those principles which had so successfully guided me in other cases.

After much consideration I selected for my test the contrivance of a machine that should be able to play a game of purely intellectual skill successfully ; such as tit-tat-to, drafts, chess, &c.

I endeavoured to ascertain the opinions of persons in every class of life and of all ages, whether they thought it required human reason to play games of skill. The almost constant answer was in the affirmative. Some supported this view of the case by observing, that if it were otherwise, then an automaton could play such games. A few of those who had considerable acquaintance with mathematical science allowed the possibility of machinery being capable of such work; but they most stoutly denied the possibility of contriving such machinery on account of the myriads of combinations which even the simplest games included.

On the first part of my inquiry I soon arrived at a demonstration that every game of skill is susceptible of being played by an automaton.

Further consideration showed that if any position of the men upon the board were assumed (whether that position were possible or impossible), then if the automaton could make the first move rightly, he must be able to win the game, always supposing that, under the given position of the men, that conclusion were possible.

⊕
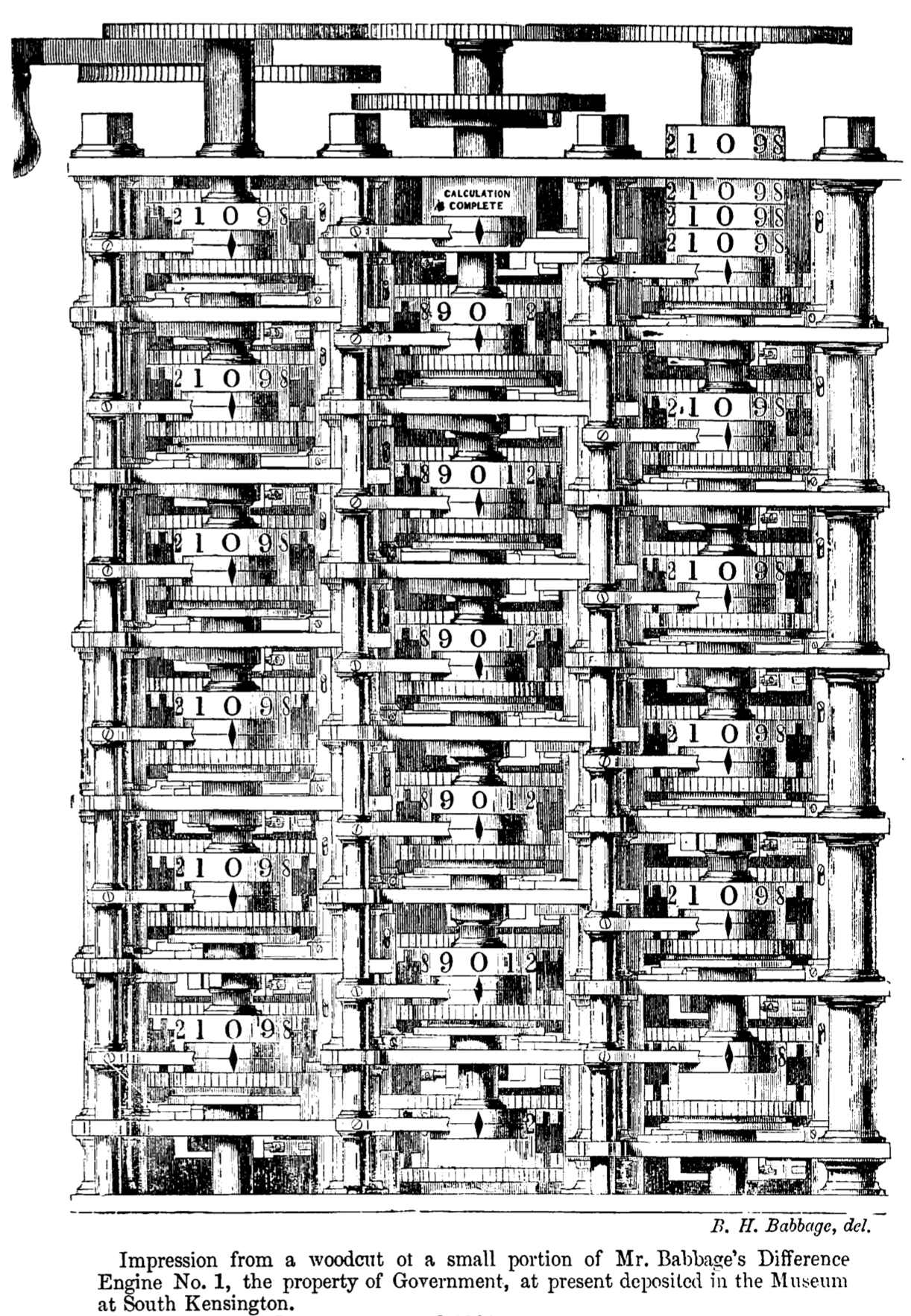
Babbage’s Difference Engine, a woodcut from Passages from the Life of a Philosopher

Whatever move the automaton made, another move would be made by his adversary. Now this altered state of the board is one amongst the many positions of the men in which, by the previous paragraph, the automaton was supposed capable of acting.

Hence the question is reduced to that of making the best move under any possible combinations of positions of the men.

Now the several questions the automaton has to consider are of this nature: –

1. Is the position of the men, as placed before him on the board, a possible position? that is, one which is consistent with the rules of the game?
2. If so, has Automaton himself already lost the game?
3. If not then has Automaton won the game?
4. If not, can he win it at the next move? If so, make that move.
5. If not, could his adversary, if he had the move, win the game.
6. If so, Automaton must prevent him if possible.
7. If his adversary cannot win the game at his next move, Automaton must examine whether he can make such a move that, if he were allowed to have two moves in succession, he could at the second move have two different ways of winning the game;

and each of these cases failing, Automaton must look forward to three or more successive moves.

Now I have already stated that in the Analytical Engine I had devised mechanical means equivalent to memory, also that I had provided other means equivalent to foresight, and that the Engine itself could act on this foresight.

In consequence of this the whole question of making an automaton play any game depended upon the possibility of the machine being able to represent all the myriads of combinations relating to it. Allowing one hundred moves on each side for the longest game at chess, I found that the combinations involved in the Analytical Engine enormously surpassed any required, even by the game of chess.

As soon as I had arrived at this conclusion I commenced an examination of a game called “tit-tat-to,”Tic-tac-toe usually played by little children. It is the simplest game with which I am acquainted.

… The next step I made was to ascertain what number of combinations were required for all the possible variety of moves and situations. I found this to be comparatively insignificant.

⊕
The animatronic lamb, Francis, coming to audition for a role in Babbage’s machine with his father, Frank. Once imagined to have an important role in promoting artificial intelligence, animatronic animals have now been reduced to playing roles in television commercials. (source)

I therefore easily sketched out mechanism by which such an automaton might be guided. Hitherto I had considered only the philosophical view of the subject, but a new idea now entered my head which seemed to offer some chance of enabling me to acquire the funds necessary to complete the Analytical Engine.

It occurred to me that if an automaton were made to play this game, it might be surrounded with such attractive circumstances that a very popular and profitable exhibition might be produced. I imagined that the machine might consist of the figures of two children playing against each other, accompanied by a lamb and a cock. That the child who won the game might clap his hands whilst the cock was crowing, after which, that the child who was beaten might cry and wring his hands whilst the lamb began bleating.

I then proceeded to sketch various mechanical means by which every action could be produced. These, when compared with those I had employed for the Analytical Engine, were remarkably simple.

… An inquiring spectator, who observed the games played by the automaton, might watch a long time before he discovered the principle upon which it acted. It is also worthy of remark how admirably this illustrates the best definitions of chance by the philosopher and the poet :–

“Chance is but the expression of man’s ignorance.” — Laplace

“All chance, design ill understood.” — Pope

Having fully satisfied myself of the power of making such an automaton, the next step was to ascertain whether there was any probability, if it were exhibited to the public, of its producing, in a moderate time, such a sum of money as would enable me to construct the Analytical Engine. A friend, to whom I had at an early period communicated the idea, entertained great hopes of its pecuniary success. When it became known that an automaton could beat not merely children but even papa and mamma at a child’s game, it seemed not unreasonable to expect that every child who heard of it would ask mamma to see it. On the other hand, every mamma, and some few papas, who heard of it would doubtless take their children to so singular and interesting a sight. I resolved, on my return to London, to make inquiries as to the relative productiveness of the various exhibitions of recent years, and also to obtain some rough estimate of the probable time it would take to construct the automaton, as well as some approximation to the expense.

⊕
The Automaton Exhibition, Gothic Hall, Haymarket (source: Wikipedia)

It occurred to me that if half a dozen were made, they might be exhibited in three different places at the same time. Each exhibitor might then have an automaton in reserve in case of accidental injury. On my return to town I made the inquiries I alluded to, and found that the English machine for making Latin verses, the German talking-machine, as well as several others, were entire failures in a pecuniary point of view. I also found that the most profitable exhibition which had occurred for many years was that of the little dwarf, General Tom Thumb.

On considering the whole question, I arrived at the conclusion, that to conduct the affair to a successful issue it would occupy so much of my own time to contrive and execute the machinery, and then to superintend the working out of the plan, that even if successful in point of pecuniary profit, it would be too late to avail myself of the money thus acquired to complete the Analytical Engine.

Aside from the interesting discussion of an automaton mimicking an intelligence playing a game, Babbage mentions in passing the interesting difficulty in distinguishing chance from an inscrutable algorithm. But separating Babbage’s deeper theoretical points from the background chatter is difficult, which explains why he was largely ignored by theoreticians. Even when attempting theoretical rigor when discussing the universality of his proposed Analytical Engine, Babbage seems to rely on too much hand-waving:

⊕Passages from the Life of a Philospher, pp. 122-128 The Analytical Engine first computes and punches on cards its own tabular numbers. These are brought to it by its attendant when demanded. But the engine itself takes care that the right card is brought to it by verifying the number of that card by the number of the card which it demanded. The Engine will always reject a wrong card by continually ringing a loud bell and stopping itself until supplied with the precise intellectual food it demands.

⊕
“To those who are acquainted with the principles of the Jacquard loom, and who are also familiar with analytical formulæ, a general idea of the means by which the Engine executes its operations may be obtained without much difficulty. In the Exhibition of 1862 there were many splendid examples of such looms. It is known as a fact that the Jacquard loom is capable of weaving any design which the imagination of man may conceive. It is also the constant practice for skilled artists to be employed by manufacturers in designing patterns. These patterns are then sent to a peculiar artist, who, by means of a certain machine, punches holes in a set of pasteboard cards in such a manner that when those cards are placed in a Jacquard loom, it will then weave upon its produce the exact pattern designed by the artist.” Charles Babbage, “Weaving Formulæ”, Passages from the Life of a Philosopher, pp. 116-117 Machines like this one helped inspire both the computer and the communist revolutions (source: Wikipedia)

… Supposing the velocity of the moving parts of the Engine to be not greater than forty feet per minute, I have no doubt that

Sixty additions or subtractions may be completed and printed in one minute.

One multiplication of two numbers, each of fifty figures, in one minute.

One division of a number having 100 places of figures by another of 50 in one minute.

In the various sets of drawings of the modifications of the mechanical structure of the Analytical Engines, already numbering upwards of thirty, two great principles were embodied to an unlimited extent.

1st. The entire control over arithmetical operations, however large, and whatever might be the number of their digits.

2nd. The entire control over the combinations of algebraic symbols, however lengthened those processes may be required. The possibility of fulfilling these two conditions might reasonably be doubted by the most accomplished mathematician as well as by the most ingenious mechanician.

The difficulties which naturally occur to those capable of examining the question, as far as they relate to arithmetic, are these, —

(a). The number of digits in each constant inserted in the Engine must be without limit.

(b). The number of constants to be inserted in the Engine must also be without limit,

(c). The number of operations necessary for arithmetic is only four, but these four may be repeated an unlimited number of times.

(d). These operations may occur in any order, or follow an unlimited number of laws.

The following conditions relate to the algebraic portion of the Analytical Engine:—

(e). The number of literal constants must be unlimited.

(f). The number of variables must be without limit.

(g). The combinations of the algebraic signs must be unlimited.

(h). The number of functions to be employed must be without limit.

… Now it is obvious that no finite machine can include infinity. It is also certain that no question necessarily involving infinity can ever be converted into any other in which the idea of infinity under some shape or other does not enter.

It is impossible to construct machinery occupying unlimited space ; but it is possible to construct finite machinery, and to use it through unlimited time. It is this substitution of the infinity of time for the infinity of space which I have made use of, to limit the size of the engine and yet to retain its unlimited power.

… The last condition (h), namely, that the number of functions to be employed must be without limit, might seem at first sight to be difficult to fulfil. But when it is considered that any function of any number of operations performed upon any variables is but a combination of the four simple signs of operation with various quantities, it becomes apparent that any function whatever may be represented by two groups of cards, the first being signs of operation, placed in the order in which they succeed each other, and the second group of cards representing the variables and constants placed in the order of succession in which they are acted upon by the former.

Thus it appears that the whole of the conditions which enable a finite machine to make calculations of unlimited extent are fulfilled in the Analytical Engine. The means I have adopted are uniform. I have converted the infinity of space, which was required by the conditions of the problem, into the infinity of time. The means I have employed are in daily use in the art of weaving patterns.

While Babbage makes some interesting points, he papers over some of the biggest difficulties that would occupy the minds of mathematicians in the following century. For example, why is it that the four arithmetic operations suffice to define all functions as their combination? Are all four necessary? Babbage doesn’t even try to investigate in any rigor. Instead, he refers the reader to others who may better advocate on his behalf.

In 1842, an Italian general and mathematician by the name of Luigi Menabrea (1809-1896) wrote an article about Babbage’s proposed Analytical Engine. Here is an excerpt:

⊕L. F. Menabrea, translated by Ada Augusta, Countess of Lovelace, Sketch of the Analytical Engine Invented by Charles Babbage, 1842, in Morrison, Charles Babbage and his Calculating Engines pp. 243-244 Considered under the most general point of view, the essential object of the machine being to calculate, according to the laws dictated to it, the values of numerical coefficients which it is then to distribute appropriately on the columns which represent the variables, it follows that the interpretation of formulae and of results is beyond its province, unless indeed this very interpretation be itself susceptible of expression by means of the symbols which the machine employs. Thus, although it is not itself the being that reflects, it may yet be considered as the being which executes the conceptions of intelligence.Here Lovelace, the translator, refers the reader to her note G, below. The cards receive the impress of these conceptions, and transmit to the various trains of mechanism composing the engine the orders necessary for their action. When once the engine shall have been constructed, the difficulty will be reduced to the making out of the cards; but as these are merely the translation of algebraical formulæ, it will, by means of some simple notations, be easy to consign the execution of them to a workman. Thus the whole intellectual labour will be limited to the preparation of the formulæ, which must be adapted for calculation by the engine.

Now, admitting that such an engine can be constructed, it may be inquired: what will be its utility? To recapitulate; it will afford the following advantages:—First, rigid accuracy. We know that numerical calculations are generally the stumbling-block to the solution of problems, since errors easily creep into them, and it is by no means always easy to detect these errors. Now the engine, by the very nature of its mode of acting, which requires no human intervention during the course of its operations, presents every species of security under the head of correctness: besides, it carries with it its own check; for at the end of every operation it prints off, not only the results, but likewise the numerical data of the question; so that it is easy to verify whether the question has been correctly proposed. Secondly, economy of time: to convince ourselves of this, we need only recollect that the multiplication of two numbers, consisting each of twenty figures, requires at the very utmost three minutes. Likewise, when a long series of identical computations is to be performed, such as those required for the formation of numerical tables, the machine can be brought into play so as to give several results at the same time, which will greatly abridge the whole amount of the processes. Thirdly, economy of intelligence: a simple arithmetical computation requires to be performed by a person possessing some capacity; and when we pass to more complicated calculations, and wish to use algebraical formulae in particular cases, knowledge must be possessed which presupposes preliminary mathematical studies of some extent. Now the engine, from its capability of performing by itself all these purely material operations, spares intellectual labour, which may be more profitably employed. Thus the engine may be considered as a real manufactory of figures, which will lend its aid to those many useful sciences and arts that depend on numbers. Again, who can foresee the consequences of such an invention? In truth, how many precious observations remain practically barren for the progress of the sciences, because there are not powers sufficient for computing the results! And what discouragement does the perspective of a long and arid computation cast into the mind of a man of genius, who demands time exclusively for meditation, and who beholds it snatched from him by the material routine of operations! Yet it is by the laborious route of analysis that he must reach truth; but he cannot pursue this unless guided by numbers; for without numbers it is not given us to raise the veil which envelopes the mysteries of nature. Thus the idea of constructing an apparatus capable of aiding human weakness in such researches, is a conception which, being realized, would mark a glorious epoch in the history of the sciences.

Babbage writes:

⊕Passages from the Life of a Philospher, p. 136 The elementary principles on which the Analytical Engine rests were thus in the first instance brought before the public by General Menabrea. Some time after the appearance of his memoir on the subject in the “Bibliothèque Universelle de Genève,” the late Countess of Lovelace informed me that she had translated the memoir of Menabrea. I asked why she had not herself written an original paper on a subject with which she was so intimately acquainted ? To this Lady Lovelace replied that the thought had not occurred to her. I then suggested that she should add some notes to Menabrea’s memoir; an idea which was immediately adopted.

… These two memoirs taken together furnish, to those who are capable of understanding the reasoning, a complete demonstration—That the whole of the developments and operations of analysis are now capable of being executed by machinery.

In the notes accompanying her translation of Menabrea’s article (which are much longer than the article itself) and describing both the mechanical and theoretical underpinnings of Babbage’s machine — notes that included what is considered today to be the first computer program (not quoted here) — Ada Lovelace (1815 – 1852) says this about the theoretical aspects of computation:

⊕Sketch of the Analytical Engine Invented by Charles Babbage With notes upon the Memoir by the Translator Ada Augusta, Countess of Lovelace, 1842, in Morrison, Charles Babbage and his Calculating Engines pp. 247-256

Note A

… In studying the action of the Analytical Engine, we find that the peculiar and independent nature of the considerations which in all mathematical analysis belong to operations, as distinguished from the objects operated upon and from the results of the operations performed upon those objects, is very strikingly defined and separated.

It is well to draw attention to this point, not only because its full appreciation is essential to the attainment of any very just and adequate general comprehension of the powers and mode of action of the Analytical Engine, but also because it is one which is perhaps too little kept in view in the study of mathematical science in general. It is, however, impossible to confound it with other considerations, either when we trace the manner in which that engine attains its results, or when we prepare the data for its attainment of those results. It were much to be desired, that when mathematical processes pass through the human brain instead of through the medium of inanimate mechanism, it were equally a necessity of things that the reasonings connected with operations should hold the same just place as a clear and well-defined branch of the subject of analysis, a fundamental but yet independent ingredient in the science, which they must do in studying the engine. The confusion, the difficulties, the contradictions which, in consequence of a want of accurate distinctions in this particular, have up to even a recent period encumbered mathematics in all those branches involving the consideration of negative and impossible quantities, will at once occur to the reader who is at all versed in this science, and would alone suffice to justify dwelling somewhat on the point, in connexion with any subject so peculiarly fitted to give forcible illustration of it as the Analytical Engine. It may be desirable to explain, that by the word operation, we mean any process which alters the mutual relation of two or more things, be this relation of what kind it may. This is the most general definition, and would include all subjects in the universe. In abstract mathematics, of course operations alter those particular relations which are involved in the considerations of number and space, and the results of operations are those peculiar results which correspond to the nature of the subjects of operation. But the science of operations, as derived from mathematics more especially, is a science of itself, and has its own abstract truth and value; just as logic has its own peculiar truth and value, independently of the subjects to which we may apply its reasonings and processes. Those who are accustomed to some of the more modern views of the above subject, will know that a few fundamental relations being true, certain other combinations of relations must of necessity follow; combinations unlimited in variety and extent if the deductions from the primary relations be carried on far enough. They will also be aware that one main reason why the separate nature of the science of operations has been little felt, and in general little dwelt on, is the shifting meaning of many of the symbols used in mathematical notation.

… The operating mechanism can even be thrown into action independently of any object to operate upon (although of course no result could then be developed). Again, it might act upon other things besides number, were objects found whose mutual fundamental relations could be expressed by those of the abstract science of operations, and which should be also susceptible of adaptations to the action of the operating notation and mechanism of the engine. Supposing, for instance, that the fundamental relations of pitched sounds in the science of harmony and of musical composition were susceptible of such expression and adaptations, the engine might compose elaborate and scientific pieces of music of any degree of complexity or extent.

The Analytical Engine is an embodying of the science of operations, constructed with peculiar reference to abstract number as the subject of those operations.

… The calculus of operations is likewise in itself a topic of so much interest, and has of late years been so much more written on and thought on than formerly, that any bearing which that engine, from its mode of constitution, may possess upon the illustration of this branch of mathematical science should not be overlooked. Whether the inventor of this engine had any such views in his mind while working out the invention, or whether he may subsequently ever have regarded it under this phase, we do not know; but it is one that forcibly occurred to ourselves on becoming acquainted with the means through which analytical combinations are actually attained by the mechanism. We cannot forbear suggesting one practical result which it appears to us must be greatly facilitated by the independent manner in which the engine orders and combines its operations: we allude to the attainment of those combinations into which imaginary quantities enter. … It seems to us obvious, however, that where operations are so independent in their mode of acting, it must be easy, by means of a few simple provisions, and additions in arranging the mechanism, to bring out a double set of results, viz.— 1st, the numerical magnitudes which are the results of operations performed on numerical data. (These results are the primary object of the engine.) 2ndly, the symbolical results to be attached to those numerical results, which symbolical results are not less the necessary and logical consequences of operations performed upon symbolical data, than are numerical results when the data are numerical.

… The former engineLovelace is referring here to Babbage’s difference engine. is in its nature strictly arithmetical, and the results it can arrive at lie within a very clearly defined and restricted range, while there is no finite line of demarcation which limits the powers of the Analytical Engine. These powers are co-extensive with our knowledge of the laws of analysis itself, and need be bounded only by our acquaintance with the latter. Indeed we may consider the engine as the material and mechanical representative of analysis, and that our actual working powers in this department of human study will be enabled more effectually than heretofore to keep pace with our theoretical knowledge of its principles and laws, through the complete control which the engine gives us over the executive manipulation of algebraical and numerical symbols.

⊕
Lophophora williamsii or Peyote. Lovelace suggests computers as an alternative entheogen. (Source: Wikipedia)

Those who view mathematical science, not merely as a vast body of abstract and immutable truths, whose intrinsic beauty, symmetry and logical completeness, when regarded in their connexion together as a whole, entitle them to a prominent place in the interest of all profound and logical minds, but as possessing a yet deeper interest for the human race, when it is remembered that this science constitutes the language through which alone we can adequately express the great facts of the natural world, and those unceasing changes of mutual relationship which, visibly or invisibly, consciously or unconsciously to our immediate physical perceptions, are interminably going on in the agencies of the creation we live amidst: those who thus think on mathematical truth as the instrument through which the weak mind of man can most effectually read his Creator’s works, will regard with especial interest all that can tend to facilitate the translation of its principles into explicit practical forms.

⊕
Ada Lovelace inspired by a mechanical loom, from Ada Lovelace, Poet of Science: The First Computer Programmer

The distinctive characteristic of the Analytical Engine, and that which has rendered it possible to endow mechanism with such extensive faculties as bid fair to make this engine the executive right-hand of abstract algebra, is the introduction into it of the principle which Jacquard devised for regulating, by means of punched cards, the most complicated patterns in the fabrication of brocaded stuffs. It is in this that the distinction between the engines lies… We may say most aptly, that the Analytical Engine weaves algebraical patterns just as the Jacquard-loom weaves flowers and leaves.

… The bounds of arithmetic were… outstepped the moment the idea of applying the cards had occurred; and the Analytical Engine does not occupy common ground with mere “calculating machines”. It holds a position wholly its own; and the considerations it suggests are most interesting in their nature. In enabling mechanism to combine together general symbols in successions of unlimited variety and extent, a uniting link is established between the operations of matter and the abstract mental processes of the most abstract branch of mathematical science. A new, a vast, and a powerful language is developed for the future use of analysis, in which to wield its truths so that these may become of more speedy and accurate practical application for the purposes of mankind than the means hitherto in our possession have rendered possible. Thus not only the mental and the material, but the theoretical and the practical in the mathematical world, are brought into more intimate and effective connexion with each other. We are not aware of its being on record that anything partaking in the nature of what is so well designated the Analytical Engine has been hitherto proposed, or even thought of, as a practical possibility, any more than the idea of a thinking or of a reasoning machine.

We will touch on another point which constitutes an important distinction in the modes of operating of the Difference and Analytical Engines. In order to enable the former to do its business, it is necessary to put into its columns the series of numbers constituting the first terms of the several orders of differences for whatever is the particular table under consideration. The machine then works upon these as its data. But these data must themselves have been already computed through a series of calculations by a human head. Therefore that engine can only produce results depending on data which have been arrived at by the explicit and actual working out of processes that are in their nature different from any that come within the sphere of its own powers. In other words, an analysing process must have been gone through by a human mind in order to obtain the data upon which the engine then synthetically builds its results. The Difference Engine is in its character exclusively synthetical, while the Analytical Engine is equally capable of analysis or of synthesis.

… Those who incline to very strictly utilitarian views may perhaps feel that the peculiar powers of the Analytical Engine bear upon questions of abstract and speculative science, rather than upon those involving every-day and ordinary human interests. These persons being likely to possess but little sympathy, or possibly acquaintance, with any branches of science which they do not find to be useful (according to their definition of that word), may conceive that the undertaking of that engine, now that the other one is already in progress, would be a barren and unproductive laying out of yet more money and labour; in fact, a work of supererogation. Even in the utilitarian aspect, however, we do not doubt that very valuable practical results would be developed by the extended faculties of the Analytical Engine; some of which results we think we could now hint at, had we the space; and others, which it may not yet be possible to foresee, put which would be brought forth by the daily increasing requirements of science, and by a more intimate practical acquaintance with the powers of the engine, were it in actual existence.

…

⊕p. 284 Note G

It is desirable to guard against the possibility of exaggerated ideas that might arise as to the powers of the Analytical Engine. In considering any new subject, there is frequently a tendency, first, to overrate what we find to be already interesting or remarkable; and, secondly, by a sort of natural reaction, to undervalue the true state of the case, when we do discover that our notions have surpassed those that were really tenable.

The Analytical Engine has no pretensions whatever to originate anything. It can do whatever we know how to order it to perform. It can follow analysis; but it has no power of anticipating any analytical relations or truths. Its province is to assist us in making available what we are already acquainted with. This it is calculated to effect primarily and chiefly of course, through its executive faculties; but it is likely to exert an indirect and reciprocal influence on science itself in another manner. For, in so distributing and combining the truths and the formulre of analysis, that they may become most easily and rapidly amenable to the mechanical combinations of the engine, the relations and the nature of many subjects in that science are necessarily thrown into new lights, and more profoundly investigated. This is a decidedly indirect, and a somewhat speculative, consequence of such an invention. It is however pretty evident, on general principles, that in devising for mathematical truths a new form in which to record and throw themselves out for actual use, views are likely to be induced, which should again react on the more theoretical phase of the subject. There are in all extensions of human power, or additions to human knowledge, various collateral influences, besides the main and primary object attained.

While Lovelace’s philosophical analysis is, no doubt, deeper than Babbage’s, it, too, has the air of recognized potential more than a rigorous analysis. It does, however, contain some significant points of interest. First, Lovelace describes what she calls operation and today we’d call computation as “any process which alters the mutual relation of two or more things, be this relation of what kind it may. This is the most general definition, and would include all subjects in the universe,” and seems to hint at what we today call the physical Church-Turing thesis (which Babbage took to mean “[t]hat the whole of the developments and operations of analysis are now capable of being executed by machinery”). But she then backs away from such extreme universality and rejects not only Leibniz’s conjecture that the mind is a divinely-built computer — and what would be Turing’s certainty about the “mere” computational nature of intelligenceTuring tackles Lovelace’s ‘objection’ in his 1950 Computing Machinery and Intelligence — but even finds it necessary to qualify what Manabrea refers to as “the conceptions of intelligence,” which she fears may lead to “exaggerated ideas”. She insists that, “[t]he Analytical Engine has no pretensions whatever to originate anything. … It can follow analysis; but it has no power of anticipating any analytical relations or truths.” Indeed, it is the precise distinction between the operation of the mind and that of the machine is the main cause for the “confusion, the difficulties, the contradictions” in understanding computation. She does not share Leibniz’s observation about our “blind thoughts”.

In fact, Lovelace describes a very distinct hierarchy, of three tiers: arithmetic, “analysis” and intelligence, whose first tier is inhabited by the difference engine, the second by the analytical engine, and the third by humans alone. She writes, “The bounds of arithmetic were… outstepped the moment the idea of applying the cards had occurred; and the Analytical Engine does not occupy common ground with mere ‘calculating machines’. It holds a position wholly its own.” And the reason for that is that, “[i]n enabling mechanism to combine together general symbols in successions of unlimited variety and extent, a uniting link is established between the operations of matter and the abstract mental processes of the most abstract branch of mathematical science.” In one of the notes (not quoted above), she repeats this idea that abstract mathematics requires faculties above and beyond mere arithmetic: “It has been observed in some of the former Notes, that the processes used in analysis form a logical system of much higher generality than the applications to number merely.” Perhaps it was Peacock’s reframing of algebra as a science independent of arithmetic and superior to it thanks to its abstract and more universal nature that caused Ada Lovelace to believe that a distinct and “higher” computational faculty was required for former than for the latter.

Charles Babbage’s son, Henry Babbage (1824-1918), continued working on the Analytical Engine after his father’s death in 1871, completing the construction of some parts of the machine. In 1878, a committee of the British Association for the Advancement of Science was “appointed to consider the advisability and to estimate the expense of constructing Mr. Babbage’s Analytical Machine, and of printing Tables by its means.” Here is an excerpt of its final report, submitted in 1879:

⊕Report of the Committee, consisting of Professor Cayley, Dr. Farr, Mr. J. W. L. Glaisher, Dr. Pole, Professor Fuller, Professor A. B. W. Kennedy, Professor Clifford, and Mr. C. W. Merrrifield, appointed to consider the advisability and to estimate the expense of constructing Mr. Babbage’s Analytical Machine, and of printing Tables by its means. Drawn up by Mr. Merrrifield. in Randell, The Origins of Digital Computers: Selected Papers, pp. 63-65 If all sorts of heavy work of this kind could be easily and quickly, as well as certainly, done, by merely selecting or punching a few Jacquard cards and turning a handle, not only much saving of labour would result, but much which is now out of hnman possibility would be brought within easy reach.

If intelligently directed and saved from wasteful use, such a machine might mark an era in the history of computation, as decided as the introduction of logarithms in the seventeenth century did in trigonometrical and astronomical arithmetic. Care might be required to guard against misuse, especially against the imposition of Sisyphean tasks upon it by influential sciolists. This, however, is no more than has happened in the history of logarithms. Much work has been done with them which could more easily have been done without them, and the old reproach is probably true, that more work has been spent upon making tables than has been saved by their use. Yet, on the whole, there can be no reasonable doubt that the first calculation of logarithmic tables was an expenditure of capital which has repaid itself over and over again. So probably would the analytical engine, whatever its cost, if we could be assured of its success.

…

General Conclusions, and Recommendation.

1. We are of opinion that the labours of Mr. Babbage, firstly on his Difference Engine, and secondly on his Analytical Engine, are a marvel of mechanical ingenuity and resource.
2. We entertain no doubt as to the utility of such an engine as was in his contemplation when he undertook the invention of his analytical engine, supposing it to be successfully constructed and maintained in efficiency.
3. We do not consider that the possibilities of its misuse are any serious drawback to its use or value.
4. Apart, from the question of its saving labour in operations now possible, we think the existence of such an instrument would place within reach much which, if not actually impossible, has been too close to the limits of human skill and endurance to be practically available.
5. We have come to the conclusion that in the present state of the design of the engine it is not possible for us to form any reasonable estimate of its cost, or of its strength and durability.
6. We are also of opinion that, in the present state of the design, it is not more than a theoretical possibility; that is to say, we do not consider it a certainty that it could be constructed and put together so as to run smoothly and correctly, and to do the work expected of it.

…

11. Having regard to all these considerations, we have come, not without reluctance, to the conclusion, that we cannot advise the British Association to take any steps, either by way of recommendation or otherwise, to procure the construction of Mr. Babbage’s Analytical Engine and the printing tables by its means.

The Monist

In the second half of the nineteenth century, logic experienced a resurgence, and while progress isn’t made in a vacuum, there is little doubt that the man most responsible for that revival was a self-taught mathematician born into poverty, George Boole (1815-1864).

At this point I’m afraid I must pause the narrative — before even starting with some biographical details of Boole’s life, for reasons that will become apparent — and make a slight methodological detour. While my assumption is that the reader has some basic knowledge of mathematics, there is some terminological confusion surrounding Boolean algebra — an algebra largely based on the one created by Boole, and one of the most important mathematical breakthroughs of the nineteenth century. Wikipedia makes matters worse by having two separate entries for Boolean algebra, with two conflicting definitions, one of those entries containing both conflicting definition. While the familiar algebra of truth values with truth-table operations, of the elements 1 and 0, is indeed, a Boolean algebra — the smallest one, in fact — it does not at all convey the general Boolean algebra. The general Boolean algebra is explained in this Wikipedia article, but I will very briefly explain some of the basics as we encounter them. At this point I will just mention that the easiest way to understand Boolean algebra is to think of it as an algebraic structure (a set of elements with some operations on them) whose elements are subsets of some arbitrary non-empty set called the universe, the element 0 represents the empty (sub)set, 1 represents the universe set, and the operations or and and correspond to union and intersection respectively (although, as we’ll see, Boole’s algebra differs from Boolean algebra in one important aspect, which caused much controversy). It is this algebra, and not the one composed of just the two elements, 0 and 1, that makes it able to represent Aristotelian logic.

Ivor Grattan-Guinness, a historian of logic and mathematics, writes:

⊕Landmark Writings in Western Mathematics, p. 476 For Boole an important aspect of his logic was its connection with religion. During his adult career British Christianity was in a state of considerable ferment, with the strong rise of Dissenting versions competing with each other and with the established Church of England. Boole belonged to one of these factions: ecumenism, which advocated the One and Only God in contrast to establishment Trinitarianism. This stance was reflected in his logic by the status of the universe 1, to be divided into its components. The link was exhibited in The Laws of Thought, though without announcement and so overlooked by most readers. The clearest evidence is provided in ch. 13, where he provided logical analyses of propositions due to Samuel Clarke and Benedict Spinoza concerning the necessary existence of ‘Some one unchangeable and independent Being’. He also alluded to his position in print very discreetly a few lines from the end of the book, where he referred to ‘those who profess an intellectual allegiance to the Father of Lights’, one of the standard Dissenter names of the Godhead (not God as Orthodoxedly construed). He greatly admired the book Philosophie— Logique (1855) of Father A. Gratry, who larded his own version of logic with religious fervour.

To Boole, and also to his wife Mary (whom he married in 1855) the hero was Frederick Denison Maurice (1805–1872), who advocated ecumenism with great force in mid century and so was dismissed from his chair of Divinity at King’s College London. Boole spent parts of several summer vacations in England in his last years, studying in London libraries—and on the Sundays he attended Maurice’s services. The strength of his admiration was exhibited in his last days. Late in November 1864 he walked to the University in the rain without protection, and after lecturing in wet clothes he soon developed pneumonia. As he lay at home on his deathbed, he asked that a portrait of Maurice be set up alongside.

This interpretation of Boole’s logic was influential only upon his widow, who continued to prosecute it and especially the educational aspects of his philosophy after his death. In penury after his death with five young daughters to bring up, she obtained employment for some years from Maurice in Queen’s College, an establishment for female education that he had established in London.

In a 1901 letter, Mary Everest Boole (1832-1916), George’s wife, who was herself a mathematician and a feminist philosopher, writes:

⊕Indian Thought and Western Science in the Nineteenth Century, p. 4 My husband told me that when he was a lad of seventeen a thought struck him suddenly, which became the foundation of all his future discoveries. It was a flash of psychological insight into the conditions under which a mind most readily accumulates knowledge. Many young people have similar flashes of revelation as to the nature of their own mental powers; those to whom they occur often become distinguished in some branch of learning; but to no one individual does the revelation come with sufficient clearness to enable him to explain to others the true secret of his success. George Boole, poor and with little leisure for study, became known as a learned and original mathematician at an early age. From the first he connected his scrap of psychologic knowledge with sacred literature. For a few years he supposed himself to be convinced of the truth of “the Bible” as a whole, and even intended to take orders as a clergyman of the English Church. But by the help of a learned Jew in Lincoln he found out the true nature of the discovery which had dawned on him. This was that man’s mind works by means of some mechanism which “functions normally towards Monism.” Besides the information which reaches it from the external world, it receives knowledge direct from The Unseen every time it returns to the thought of Unity between any given elements (of fact or thought), after a period of tension on the contrast or antagonism between those same elements.

In other words, while it is intuitively reasonable to use 0 to represent the “empty” or “nothing” (“bottom”, in modern terms) element, there were, as we’ll see, different and possibly more intuitive proposals for the representation of the “universe” or “everything” (“top” in modern terms) element. But Boole liked the representation of 1, as it stand for the unity and totality of God (there are mathematical reasons, as wellIn Boolean algebra, multiplication represents intersection, and the fact that intersecting a set with the universe-set is equal to the original set is represented by the equation $xu = x$, which holds for all $x$. Since Boole, as we’ll see, wanted to keep his algebra as similar to the ordinary algebra on numbers, it makes sense to represent $u$ as 1. In category theory, initial and terminal objects are generalizations of bottom and top elements, and it just so happens that in the category whose objects correspond to sets and morphisms correspond to functions, the initial object is the one corresponding to the empty set, i.e., the set with zero elements, while the terminal objects correspond to sets with exactly one element. This, however, is rather close to being a mathematical coincidence, as this category does not represent a Boolean algebra; in the appropriate category, the morphisms correspond to the inclusion relation, and while the initial object still corresponds to the empty set, the terminal object, if it exists, usually does not correspond to a set with a single element. ).

In an 1840 letter, George Boole revealed the spiritual and religious motivations for his study of the human mind:

⊕Letter to Charles Taylor, 27 April 1840 I do not feel surprised that the latent sense of poetry should have begun to manifest itself in you while pursuing the science of the mind… I conceive it impossible that an individual should look with much fixedness of attention on the phenomenon of this inward life and being without the feeling that each observed fact each ascertained truth is but one link out of an infinite chain of possible truths of which each may afford matter for more sublime contemplation that can be derived from any of the forms of material grandeur and beauty. The ideas of human immortality of modes of being infinitely diversified and bearing no relation to our existing senses in the present life of unlimited advancement and continued development these which are among the realities of our Christian faith are also among the glorious possibilities of the science of the mind. And hence I am inclined to believe that the study of mental philosophy and the trains of reflection to which it naturally leads are favorable both to the growth of genuine poetry and the reception and appreciation of religious truth. True poetry has far more to do with man and man’s interests than with the babbling of a stream or the glittering of a dewdrop.

Because he rejected Trinitarianism, and because he considered himself a scientist of the human mind, George Boole perceived the Trinity as a myth born in the human psychology by its interaction with the physical world, with its three dimensions. Mary Boole writes:

⊕Indian Thought, pp. 4,5,7 The question next arose: What instinct in man, what fact in human psychology, has given rise to the tendency to think of the Divine as a Trinity?

The Jew could give no further help. The Trinitarian tendency was seen by George Boole in connection with the fact that man conceives the physical world in three dimensions. His Sonnet to the Number Three gives a clue to his view of this matter.

… Now you see why “Boole’s Equation”She is referring to $x^2=x$, or, its alternative formulation as $x(1 - x) = 0$. Its significance will be made clear later. seemed to me at the age of eighteen exactly what it was: the mere algebraic expression of natural psychologic truth; why I was never either puzzled or shocked by my husband’s conception of Trinity and Incarnation as myths connected with the psychology of the human mind; and why I was able to help him in his work.

… Men who were pledged to a theologic system based on the conception of three individual gods in One God, were afraid to face the simple statement that Trinity is a limitation, not of the Divine Essence, but of human concrete imagination. On the other hand, many “Free-thinkers,” proud of their emancipation from the trammels of idolatrous Trinitarian theology, shrank from all reference to Trinitarian metaphysics, as if it necessarily involved a step back towards the idolatry from which they had escaped. Those who can treat this subject sanely and reasonably are almost invariably persons who have become familiar with the Hindu conception of Trinity. They have been, however, until quite lately, in a very small minority.

Cohen writes:

⊕Equations From God, p. 77 Despite the transference of his emotional insight into the mechanics of reasoning, Boole never forgot that the notion of a mathematical logic came in the form of what he regarded as a divine manifestation, and he hoped to return the favor by applying his new logic to the advantage of religious belief. “The hope of his heart,” his wife Mary would later recall, had been “to work in the cause of true religion.” She continued, “Mathematics had never had more than a secondary interest for him; and even logic he cared for chiefly as a means of clearing the ground of doctrines imagined to be proved, by showing that the evidence on which they were supposed to rest had no tendency to prove them. But he had been endeavouring to give a more active and positive help than this to the cause of what he deemed pure religion.” The “father of pure mathematics,” as Bertrand Russell would later refer to Boole, had not been purely interested in mathematics, nor was his mathematics free of the “impurities” of extradisciplinary concerns, in particular, religious ones. The symbolic logic that is now an essential tool for secular philosophers and that forms the basis for dispassionate computers began in the mind of a warm-blooded, religiously concerned idealist.

In 1847 Boole published the pamphlet The Mathematical Analysis of Logic:

⊕The Mathematical Analysis of Logic, pp. 1-13 It appeared to me that, although Logic might be viewed with reference to the idea of quantity, it had also another and a deeper system of relations. If it was lawful to regard it from without, as connecting itself through the medium of Number with the intuitions of Space and Time, it was lawful also to regard it from within, as based upon facts of another order which have their abode in the constitution of the Mind.

… It is in the general theorems which occupy the latter chapters of this work, results to which there is no existing counterpart, that the claims of the method, as a Calculus of Deductive Reasoning, are most fully set forth.

⊕In her 1909 book, Philosophy and Fun of Algebra, Mary. E. Boole writes:
Many people think that it is impossible to make Algebra about anything except number. This is a complete mistake. We make an Algebra whenever we arrange facts that we know round a centre which is a statement of what it is that we want to know and do not know; and then proceed to deal logically with all the statements, including the statement of our own ignorance.
Algebra can be made about anything which any human being wants to know about. Everybody ought to be able to make Algebras; and the sooner we begin the better. It is best to begin before we can talk; because, until we can talk, no one can get us into illogical habits; and it is advisable that good logic should get the start of bad.
… Always remember that the use of algebra is to free people from bondage. For instance, in the case of number: Children do their numeration, their ‘carrying,’ in tens, because primitive man had nothing to do sums with but his ten fingers.
Many children grow superstitious, and think that you cannot carry except in tens; or that it is wrong to carry in anything but tens. The use of algebra is to free them from bondage to all this superstitious nonsense, and help them to see that the numbers would come just as right if we carried in eights or twelves or twenties. It is a little difficult to do this at first, because we are not accustomed to it; but algebra helps to get over our stiffness and set habits and to do numeration on any basis that suits the matter we are dealing with.
You may some day become a teacher. If ever you are teaching a class how to set down a sum or an equation, say ‘This is my way,’ or ‘This is the way which I think you will find most convenient,’ or ‘This is the way in which the Government Inspector requires you to do the sums at present, and therefore you must learn it.’ But do not take in vain the names of great unseen powers to back up either your own limitations, or your own authority, or the Inspector’s authority. Never say, or imply, ‘Arithmetic requires you to do this; your sum will come wrong if you do it differently.’ Remember that arithmetic requires nothing from you except absolute honesty and patient work.
… [P]eople who really conduct their minds strictly according to the algebra of logic are very prone to grow kindness and honesty towards other people, without thinking about it, as a matter of taste, of choice. They like being kind and honest better than being selfish and dishonest, and they become kind and honest without thinking much about it.

… They who are acquainted with the present state of the theory of Symbolical Algebra, are aware, that the validity of the processes of analysis does not depend upon the interpretation of the symbols which are employed, but solely upon the laws of their combination. Every system of interpretation which does not affect the truth of the relations supposed, is equally admissible, and it is thus that the same process may, under one scheme of interpretation, represent the solution of a question on the properties of numbers, under another, that of a geometrical problem, and under a third, that of a problem of dynamics or optics. This principle is indeed of fundamental importance ; and it may with safety be affirmed, that the recent advances of pure analysis have been much assisted by the influence which it has exerted in directing the current of investigation.

… [T]he abstractions of the modern Analysis, not less than the ostensive diagrams of the ancient Geometry, have encouraged the notion,that Mathematics are essentially, as well as actually, the Science of Magnitude.

The consideration of that view which has already been stated, as embodying the true principle of the Algebra of Symbols, would, however, lead us to infer that this conclusion is by no means necessary. If every existing interpretation is shewn to involve the idea of magnitude, it is only by induction that we can assert that no other interpretation is possible. And it may be doubted whether our experience is sufficient to render such an induction legitimate. The history of pure Analysis is, it may be said, too recent to permit us to set limits to the extent of its applications.

… That which renders Logic possible, is the existence in our minds of general notions, our ability to conceive of a class, and to designate its individual members by a common name. The theory of Logic is thus intimately connected with that of Language. A successful attempt to express logical propositions by symbols, the laws of whose combinations should be founded upon the laws of the mental processes which they represent, would, so far, be a step toward a philosophical language… Assuming the notion of a class, we are able, from any conceivable collection of objects, to separate by a mental act, those which belong to the given class, and to contemplate them apart from the rest. Such, or a similar act of election, we may conceive to be repeated. The group of individuals left under consideration may be still further limited, by mentally selecting those among them which belong to some other recognised class, as well as to the one before contemplated.

Now the several mental operations which in the above case we have supposed to be performed, are subject to peculiar laws. It is possible to assign relations among them, whether as respects the repetition of a given operation or the succession of different ones, or some other particular, which are never violated. It is, for example, true that the result of two successive acts is unaffected by the order in which they are performed; … and there are at least two other laws which will be pointed out in the proper place. These will perhaps to some appear so obvious as to be ranked among necessary truths, and so little important as to be undeserving of special notice. And probably they are noticed for the first time in this Essay. Yet it may with confidence be asserted, that if they were other than they are, the entire mechanism of reasoning, nay the very laws and constitution of the human intellect, would be vitally changed. A Logic might indeed exist, but it would no longer be the Logic we possess.

Such are the elementary laws upon the existence of which, and upon their capability of exact symbolical expression, the method of the following Essay is founded; and it is presumed that the object which it seeks to attain will be thought to have been very fully accomplished. Every logical proposition, whether categorical or hypothetical, will be found to be capable of exact and rigorous expression, and not only will the laws of conversion and of syllogism be thence deducible, but the resolution of the most complex systems of propositions, the separation of any proposed element, and the expression of its value in terms of the remaining elements, with every subsidiary relation involved. Every process will represent deduction, every mathematical consequence will express a logical inference. The generality of the method will even permit us to express arbitrary operations of the intellect, and thus lead to the demonstration of general theorems in logic analogous, in no slight degree, to the general theorems of ordinary mathematics.

… It would be premature to speak of the value which this method may possess as an instrument of scientific investigation. I speak here with reference to the theory of reasoning, and to the principle of a true classification of the forms and cases of Logic considered as a Science. The aim of these investigations was in the first instance confined to the expression of the received logic, and to the forms of the Aristotelian arrangement, but it soon became apparent that restrictions were thus introduced, which were purely arbitrary and had no foundation in the nature of things.

… The relation in which this Essay stands at once to Logic and to Mathematics, may further justify some notice of the question which has lately been revived, as to the relative value of the two studies in a liberal education. One of the chief objections which have been urged against the study of Mathematics in general, is but another form of that which has been already considered with respect to the use of symbols in particular. And it need not here be further dwelt upon, than to notice, that if it avails anything, it applies with an equal force against the study of Logic. The canonical forms of the Aristotelian syllogism are really symbolical; only the symbols are less perfect of their kind than those of mathematics. If they are employed to test the validity of an argument, they as truly supersede the exercise of reason, as does a reference to a formula of analysis. Whether men do, in the present day, make this use of the Aristotelian canons, except as a special illustration of the rules of Logic, may be doubted; yet it cannot be questioned that when the authority of Aristotle was dominant in the schools of Europe, such applications were habitually made. And our argument only requires the admission, that the case is possible.

… Philosophy is then described as the science of a real existence and the research of causes. And that no doubt may rest upon the meaning of the word cause, it is further said, that philosophy “mainly investigates the why.” … Now we might take our stand upon the conviction of many thoughtful and reflective minds, that in the extent of the meaning above stated, Philosophy is impossible. The business of true Science, they conclude, is with laws and phenomena. The nature of Being, the mode of the operation of Cause, the why, they hold to be beyond the reach of our intelligence. But we do not require the vantage-ground of this position; nor is it doubted that whether the aim of Philosophy is attainable or not, the desire which impels us to the attempt is an instinct of our higher nature. Let it be granted that the problem which has baffled the efforts of ages, is not a hopeless one; that the “science of a real existence,” and the research of causes, “that kernel” for which “Philosophy is still militant,” do not transcend the limits of the human intellect. I am then compelled to assert, that according to this view of the nature of Philosophy, Logic forms no part of it. On the principle of a true classification, we ought no longer to associate Logic and Metaphysics, but Logic and Mathematics.

The similarity between this text and Leibniz’s work — unknown to Boole at the time, even though some of the work on the characteristica universalis and the calculus ratiocinator had been published — is truly striking, but it is not miraculous, as both explained their thought process, which was the same. Like Leibniz, Boole saw logic as an expression of the “laws of the mind,” mimicking its operations (although he did not use the word “computation”). Like Leibniz, Boole believed that “[t]he theory of Logic is thus intimately connected with that of Language”, and that the laws of the mind should be studied through the laws of language, and, like Leibniz, he seeks to create a “philosophical language.” Like Leibniz, his starting point is the superficial similarity between”the canonical forms of the Aristotelian syllogism,” that “are really symbolical” and algebra, the study of the laws of combination of symbols, noting that the symbols of Aristotelian logic “are less perfect of their kind” than those of algebra. Most importantly, both Boole and Leibniz set out to mathematize the same Aristotelian logic.

Mary Everest Boole wrote:

⊕Letters to a Reformer’s Children, 1905, in M. E. Boole, Collected Works, vol. 3, p. 1142 Some one wrote to my husband to say that in reading an old treatise by Leibnitz (who lived at the same time as Newton) he had come upon the same formula which the Cambridge people call “Boole’s Equation.” My husband looked up Leibnitz and found his equation there and was perfectly delighted! He felt as if Leibnitz had come and shaken hands with him across the centuries. Afterwards, one of my husband’s admirers and would-be “followers” tried to persuade me that Leibnitz did not understand as much, or mean as much, as Boole had done.

However, while Leibniz clearly recognized the possibility of the algebraic variables representing other notions than mere numbers, he still considered the algebraic operations to be ultimately numerical, and so required an encoding of classes (collections of objects) as numbers, whereas Boole knew that “the validity of the processes of analysis does not depend upon the interpretation of the symbols which are employed, but solely upon the laws of their combination,” and that, “[e]very system of interpretation which does not affect the truth of the relations supposed, is equally admissible,” and so an algebra could be constructed where, “the laws of whose combinations should be founded upon the laws of the mental processes which they represent.”

“What is really new in Boole’s works”, says Roman Murawski,Mechanization of Reasoning, Kindle Locations 2380-2384 “is not the idea of an un-quantitative calculus — it was already by Leibniz and Lambert — but a clear description of the essence of the formalism in which the validity of a statement ‘does not depend upon the interpretation of the symbols which are employed, but solely upon the laws of their combination’. Boole indicates here that a given formal language may be interpreted in various ways. Hence he sees logic not as an analysis of abstracts from real thoughts but rather as a formal construction for which one builds afterwords an interpretation.”

While Boole’s algebra may have been the first example of a useful non-numerical algebra, his talk of “the present state of the theory of Symbolical Algebra,” clearly refers to Peacock’s treatise, which he likely learned of through his friend and mentor Duncan F Gregory (1813 — 1844), who further generalized Peacock’s ideas, and wrote of symbolical algebra thatOn the Real Nature of Symbolical Algebra, 1838, in The Mathematical Writings of Duncan Farquharson Gregory p. 1 “it is the science which treats of the combination of operations defined not by their nature, that is, by what they are or what they do, but by the laws of combination to which they are subject”.

Also of great interest is Boole’s realization that a rigorous, mathematical treatment of logic and “the laws of thought” would require examining rules that “will perhaps to some appear so obvious as to be ranked among necessary truths, and so little important as to be undeserving of special notice”. Laws of thought different from those of that of “the human intellect” would lead to a different logic, which, “might indeed exist, but it would no longer be the Logic we possess.”

Boole came to regard The Mathematical Analysis of Logic as flawed or lacking, and repeated his philosophical and mathematical views more clearly in his most famous work — one of the foundational texts of modern logic — An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities, published in 1854:

⊕An Investigation of the Laws of Thought, pp. 1-8 The design of the following treatise is to investigate the fundamental laws of those operations of the mind by which reasoning is performed; to give expression to them in the symbolical language of a Calculus, and upon this foundation to establish the science of Logic and construct its method; to make that method itself the basis of a general method for the application of the mathematical doctrine of Probabilities; and, finally, to collect from the various elements of truth brought to view in the course of these inquiries some probable intimations concerning the nature and constitution of the human mind.

… It is designed, in the first place, to investigate the fundamental laws of those operations of the mind by which reasoning is performed. It is unnecessary to enter here into any argument to prove that the operations of the mind are in a certain real sense subject to laws, and that a science of the mind is therefore possible.

⊕To the Number Three
by George Boole, 16 May 1846

When the great Maker, on Creation bent,
Thee from thy brethren chose, and framed by thee
The world to sense revealed, yet left it free
To those whose intellectual gaze intent
Behind the veil phenomenal is sent
Space diverse, systems manifold to see
Revealed by thought alone; was it that we
In whose mysterious spirits thus are blent
Finite of sense and Infinite of thought,
Should feel how vast, how little is our store;
As yon excelling arch with orbs deep-fraught
To the light wave that dies along the shore;
That from our weakness and our strength may rise
One worship unto Him the Only Wise.

The number three was chosen to frame the world of senses — as in three dimensions — but, ‘pure thought’ may reveal many more. This was Ethel Voynich’s, the youngest of Boole’s five daughters, favorite of her father’s sonnets.

Appears in Mary Everest Boole’s Symbolical Methods of Study, p. 17, as the epigraph to the chapter, The Fairyland of Mathematics. The book was, ‘a humble attempt to reproduce in a form intelligible to young people, the thoughts of some teachers of Symbolic Method of our time.’ The preface mentions ‘G. Boole’s idea that that the perfect friendship is that which exists between two persons of exactly opposite tastes, harmonized by similar aims and views of life. In Boole’s logical equation, the $1-x$ (or not-x or polar opposite of x) must belong to, and be included in, the same ‘Universe of Thought’ as the $x$ itself.’

… But if the general truths of Logic are of such a nature that when presented to the mind they at once command assent, wherein consists the difficulty of constructing the Science of Logic? … Shall we then err in regarding that as the true science of Logic which, laying down certain elementary laws, confirmed by the very testimony of the mind, permits us thence to deduce, by uniform processes, the entire chain of its secondary consequences, and furnishes, for its practical applications, methods of perfect generality? Let it be considered whether in any science, viewed either as a system of truth or as the foundation of a practical art, there can properly be any other test of the completeness and the fundamental character of its laws, than the completeness of its system of derived truths, and the generality of the methods which it serves to establish. Other questions may indeed present themselves. Convenience, prescription, individual preference, may urge their claims and deserve attention. But as respects the question of what constitutes science in its abstract integrity, I apprehend that no other considerations than the above are properly of any value.

… There is not only a close analogy between the operations of the mind in general reasoning and its operations in the particular science of Algebra, but there is to a considerable extent an exact agreement in the laws by which the two classes of operations are conducted… There exist, indeed, certain general principles founded in the very nature of language, by which the use of symbols, which are but the elements of scientific language, is determined. To a certain extent these elements are arbitrary. Their interpretation is purely conventional: we are permitted to employ them in whatever sense we please. But this permission is limited by two indispensable conditions,–first, that from the sense once conventionally established we never, in the same process of reasoning, depart; secondly, that the laws by which the process is conducted be founded exclusively upon the above fixed sense or meaning of the symbols employed. In accordance with these principles, any agreement which may be established between the laws of the symbols of Logic and those of Algebra can but issue in an agreement of processes.

… Whence it is that the ultimate laws of Logic are mathematical in their form; why they are, except in a single point, identical with the general laws of Number; and why in that particular point they differ;–are questions upon which it might not be very remote from presumption to endeavour to pronounce a positive judgment. Probably they lie beyond the reach of our limited faculties. It may, perhaps, be permitted to the mind to attain a knowledge of the laws to which it is itself subject, without its being also given to it to understand their ground and origin, or even, except in a very limited degree, to comprehend their fitness for their end, as compared with other and conceivable systems of law. Such knowledge is, indeed, unnecessary for the ends of science, which properly concerns itself with what is, and seeks not for grounds of preference or reasons of appointment. These considerations furnish a sufficient answer to all protests against the exhibition of Logic in the form of a Calculus. It is not because we choose to assign to it such a mode of manifestation, but because the ultimate laws of thought render that mode possible, and prescribe its character, and forbid, as it would seem, the perfect manifestation of the science in any other form, that such a mode demands adoption. It is to be remembered that it is the business of science not to create laws, but to discover them. We do not originate the constitution of our own minds, greatly as it may be in our power to modify their character. And as the laws of the human intellect do not depend upon our will, so the forms of the science, of which they constitute the basis, are in all essential regards independent of individual choice.

…

⊕An Investigation of the Laws of Thought, pp. 17-19 Chapter II: Signs and their Laws

That Language is an instrument of human reason, and not merely a medium for the expression of thought, is a truth generally admitted. It is proposed in this chapter to inquire what it is that renders Language thus subservient to the most important of our intellectual faculties. In the various steps of this inquiry we shall be led to consider the constitution of Language, considered as a system adapted to an end or purpose; to investigate its elements; to seek to determine their mutual relation and dependence; and to inquire in what manner they contribute to the attainment of the end to which, as co-ordinate parts of a system, they have respect.

In proceeding to these inquiries, it will not be necessary to enter into the discussion of that famous question of the schools, whether Language is to be regarded as an essential instrument of reasoning, or whether, on the other hand, it is possible for us to reason without its aid. I suppose this question to be beside the design of the present treatise, for the following reason, viz., that it is the business of Science to investigate laws; and that, whether we regard signs as the representatives of things and of their relations, or as the representatives of the conceptions and operations of the human intellect, in studying the laws of signs, we are in effect studying the manifested laws of reasoning. If there exists a difference between the two inquiries, it is one which does not affect the scientific expressions of formal law, which are the object of investigation in the present stage of this work, but relates only to the mode in which those results are presented to the mental regard. For though in investigating the laws of signs, à posteriori, the immediate subject of examination is Language, with the rules which govern its use; while in making the internal processes of thought the direct object of inquiry, we appeal in a more immediate way to our personal consciousness,—it will be found that in both cases the results obtained are formally equivalent. Nor could we easily conceive, that the unnumbered tongues and dialects of the earth should have preserved through a long succession of ages so much that is common and universal, were we not assured of the existence of some deep foundation of their agreement in the laws of the mind itself.

The elements of which all language consists are signs or symbols….

Definition.—A sign is an arbitrary mark, having a fixed interpretation, and susceptible of combination with other signs in subjection to fixed laws dependent upon their mutual interpretation…

(1.) In the first place, a sign is an arbitrary mark. …

(2.) In the second place, it is necessary that each sign should possess, within the limits of the same discourse or process of reasoning, a fixed interpretation. The necessity of this condition is obvious, and seems to be founded in the very nature of the subject. There exists, however, a dispute as to the precise nature of the representative office of words or symbols used as names in the processes of reasoning. By some it is maintained, that they represent the conceptions of the mind alone; by others, that they represent things. The question is not of great importance here, as its decision cannot affect the laws according to which signs are employed. I apprehend, however, that the general answer to this and such like questions is, that in the processes of reasoning, signs stand in the place and fulfil the office of the conceptions and operations of the mind; but that as those conceptions and operations represent things, and the connexions and relations of things, so signs represent things with their connexions and relations; and lastly, that as signs stand in the place of the conceptions and operations of the mind, they are subject to the laws of those conceptions and operations.

… The analysis and classification of those signs by which the operations of reasoning are conducted will be considered in the following Proposition:

PROPOSITION I

All the operations of Language, as an instrument of reasoning, may be conducted by a system of signs composed of the following elements, viz.:

1st. Literal symbols, as x, y, &c., representing things as subjects of our conceptions.

2nd. Signs of operation, as +, −, ×, standing for those operations of the mind by which the conceptions of things are combined or resolved so as to form new conceptions involving the same elements.

3rd. The sign of identity, =.

And these symbols of Logic are in their use subject to definite laws, partly agreeing with and partly differing from the laws of the corresponding symbols in the science of Algebra.

…

⊕An Investigation of the Laws of Thought, pp. 28-35 Chapter III: Derivation of the laws of the symbols of logic from the laws of the operations of the human mind.

… The idealist would give to the laws of reasoning one form of expression; the sceptic, if true to his principles, another. They who regard the phænomena with which we are concerned in this inquiry as the mere successive states of the thinking subject devoid of any causal connexion, and they who refer them to the operations of an active intelligence, would, if consistent, equally differ in their modes of statement. Like difference would also result from a difference of classification of the mental faculties. Now the principle which I would here assert, as affording us the only ground of confidence and stability amid so much of seeming and of real diversity, is the following, viz., that if the laws in question are really deduced from observation, they have a real existence as laws of the human mind, independently of any metaphysical theory which may seem to be involved in the mode of their statement. They contain an element of truth which no ulterior criticism upon the nature, or even upon the reality, of the mind’s operations, can essentially affect. Let it even be granted that the mind is but a succession of states of consciousness, a series of fleeting impressions uncaused from without or from within, emerging out of nothing, and returning into nothing again,—the last refinement of the sceptic intellect,—still, as laws of succession, or at least of a past succession, the results to which observation had led would remain true. They would require to be interpreted into a language from whose vocabulary all such terms as cause and effect, operation and subject, substance and attribute, had been banished; but they would still be valid as scientific truths.

… The course which it appears to me to be expedient, under these circumstances, to adopt, is to avail myself as far as possible of the language of common discourse, without regard to any theory of the nature and powers of the mind which it may be thought to embody. For instance, it is agreeable to common usage to say that we converse with each other by the communication of ideas, or conceptions, such communication being the office of words; and that with reference to any particular ideas or conceptions presented to it, the mind possesses certain powers or faculties …. To those faculties or powers different names, as Attention, Simple Apprehension, Conception or Imagination, Abstraction, &c., have been given… Whenever, then, occasion shall occur to use these terms, I shall do so without implying thereby that I accept the theory that the mind possesses such and such powers and faculties as distinct elements of its activity. Nor is it indeed necessary to inquire whether such powers of the understanding have a distinct existence or not. We may merge these different titles under the one generic name of Operations of the human mind, define these operations so far as is necessary for the purposes of this work, and then seek to express their ultimate laws.

… It will be most convenient to distribute the more definite results of the following investigation into distinct Propositions.

PROPOSITION I.

To deduce the laws of the symbols of Logic from a consideration of those operations of the mind which are implied in the strict use of language as an instrument of reasoning.

In every discourse, whether of the mind conversing with its own thoughts, or of the individual in his intercourse with others, there is an assumed or expressed limit within which the subjects of its operation are confined. The most unfettered discourse is that in which the words we use are understood in the widest possible application, and for them the limits of discourse are co-extensive with those of the universe itself. But more usually we confine ourselves to a less spacious field. Sometimes, in discoursing of men we imply (without expressing the limitation) that it is of men only under certain circumstances and conditions that we speak, as of civilized men, or of men in the vigour of life, or of men under some other condition or relation. Now, whatever may be the extent of the field within which all the objects of our discourse are found, that field may properly be termed the universe of discourse.

Furthermore, this universe of discourse is in the strictest sense the ultimate subject of the discourse. The office of any name or descriptive term employed under the limitations supposed is not to raise in the mind the conception of all the beings or objects to which that name or description is applicable, but only of those which exist within the supposed universe of discourse. If that universe of discourse is the actual universe of things, which it always is when our words are taken in their real and literal sense, then by men we mean all men that exist; but if the universe of discourse is limited by any antecedent implied understanding, then it is of men under the limitation thus introduced that we speak. It is in both cases the business of the word men to direct a certain operation of the mind, by which, from the proper universe of discourse, we select or fix upon the individuals signified.

Exactly of the same kind is the mental operation implied by the use of an adjective. Let, for instance, the universe of discourse be the actual Universe. Then, as the word men directs us to select mentally from that Universe all the beings to which the term “men” is applicable; so the adjective “good,” in the combination “good men,” directs us still further to select mentally from the class of men all those who possess the further quality “good;” and if another adjective were prefixed to the combination “good men,” it would direct a further operation of the same nature, having reference to that further quality which it might be chosen to express.

It is important to notice carefully the real nature of the operation here described, for it is conceivable, that it might have been different from what it is. Were the adjective simply attributive in its character, it would seem, that when a particular set of beings is designated by men, the prefixing of the adjective good would direct us to attach mentally to all those beings the quality of goodness. But this is not the real office of the adjective. The operation which we really perform is one of selection according to a prescribed principle or idea. To what faculties of the mind such an operation would be referred, according to the received classification of its powers, it is not important to inquire, but I suppose that it would be considered as dependent upon the two faculties of Conception or Imagination, and Attention.

… It is equally clear that the mental operation above described is of such a nature that its effect is not altered by repetition. Suppose that by a definite act of conception the attention has been fixed upon men, and that by another exercise of the same faculty we limit it to those of the race who are white. Then any further repetition of the latter mental act, by which the attention is limited to white objects, does not in any way modify the conception arrived at, viz., that of white men. This is also an example of a general law of the mind, and it has its formal expression in the law … of the literal symbols.

… These observations will explain the process of inquiry adopted in the following Proposition. The literal symbols of Logic are universally subject to the law whose expression is $x^2 = x$. …

PROPOSITION II.

To determine the logical value and significance of the symbols 0 and 1.

The symbol 0, as used in Algebra, satisfies the following formal law,

$0 \times y = 0$, or $0y = 0$,

whatever number y may represent. That this formal law may be obeyed in the system of Logic, we must assign to the symbol 0 such an interpretation that the class represented by $0y$ may be identical with the class represented by 0, whatever the class y may be. A little consideration will show that this condition is satisfied if the symbol 0 represent Nothing. In accordance with a previous definition, we may term Nothing a class. In fact, Nothing and Universe are the two limits of class extension, for they are the limits of the possible interpretations of general names, none of which can relate to fewer individuals than are comprised in Nothing, or to more than are comprised in the Universe.

Now whatever the class y may be, the individuals which are common to it and to the class “Nothing” are identical with those comprised in the class “Nothing,” for they are none. And thus by assigning to 0 the interpretation Nothing, the law is satisfied

… Secondly, The symbol 1 satisfies in the system of Number the following law, viz.,

$1 \times y = y$, or $1y = y$,

whatever number y may represent. And this formal equation being assumed as equally valid in the system of this work, in which 1 and I represent classes, it appears that the symbol 1 must represent such a class that all the individuals which are found in any proposed class y are also all the individuals $1y$ that are common to that class y and the class represented by 1. A little consideration will here show that the class represented by 1 must be “the Universe,” since this is the only class in which are found all the individuals that exist in any class. Hence the respective interpretations of the symbols 0 and 1 in the system of Logic are Nothing and Universe. …

Proposition III.

If x represent any class of objects, then will 1 − x represent the contrary or supplementary class of objects., i.e. the class including all objects which are not comprehended in the class x.

For greater distinctness of conception let x represent the class men, and let us express, according to the last Proposition, the Universe by 1; now if from the conception of the Universe, as consisting of “men” and “not-men,” we exclude the conception of “men,” the resulting conception is that of the contrary class, “not-men.” Hence the class “not-men” will be represented by 1 − x. And, in general, whatever class of objects is represented by the symbol x, the contrary class will be expressed by 1 − x. …

Proposition IV.

That axiom of metaphysicians which is termed the principle of contradiction, and which affirms that it is impossible for any being to possess a quality, and at the same time not to possess it, is a consequence of the fundamental law of thought, whose expression is $x^2 = x$.

⊕
A sketch of a scuplture of George Boole by Antony Dufort, planned to be placed in the town of Lincoln, England, Boole’s birthplace. Boole is pointing at the equation $x^2 = x$ (source: the artist’s website)

Let us write this equation in the form

$x - x^2 = 0$,

Whence we have

$x(1-x) = 0$; (1)

both these transformations being justified by the axiomatic laws of combination and transposition. Let us, for simplicity of conception, give to the symbol x the particular interpretation of men, then $1 − x$ will represent the class: of “not-men” (Prop. III.) Now the formal product of the expressions of two classes represents that class of individuals which is common to them both. Hence $x (1 − x)$ will represent the class whose members are at once “men,” and “not men,” and the equation (1) thus express the principle, that a class whose members are at the same time men and not men does not exist. In other words, that it is impossible for the same individual to be at the same time a man and not a man. Now let the meaning of the symbol x be extended from the representing of “men,” to that of any class of beings characterized by the possession of any quality whatever; and the equation (1) will then express that it is impossible for a being to possess a quality and not to possess that quality at the same time. But this is identically that “principle of contradiction” which Aristotle has described as the fundamental axiom of all philosophy. “It is impossible that the same quality should both belong and not belong to the same thing.. . . This is the most certain of all principles.. . . Wherefore they who demonstrate refer to this as an ultimate opinion. For it is by nature the source of all the other axioms.”

⊕An Investigation of the Laws of Thought, p. 39 … Speaking generally, the symbol + is the equivalent of the conjunctions “and,” “or,” and the symbol −, the equivalent of the preposition “except.” Of the conjunctions “and” and “or,” the former is usually employed when the collection to be described forms the subject, the latter when it forms the predicate, of a proposition. “The scholar and the man of the world desire happiness,” may be taken as an illustration of one of these cases. “Things possessing utility are either productive of pleasure or preventive of pain,” may exemplify the other.

The details of Boole’s algebra are those: variables represent classes of objects; the class of all objects in the chosen universe of discourse is represented by 1, and the empty class by 0; equality is equality of members, i.e., x = y iff the classes $x$ and $y$ contain the same members; multiplication is selection, or intersection, and $1 - x$ is the complement of $x$. Boolean algebra is a lattice, and thus can be viewed through the perspective of order; that $x$ is a subclass of $y$ is written as $x \leq y$, but that is a later development by those, like Schröder, who elaborated on Boole’s algebra and invented lattice theory. In Boole’s algebra there is no order, and that $x$ is a subclass of $y$ is represented by the equation $xy = x$. The syllogism “all men are animals; all animals are mortal — therefore all men are mortal”, becomes a simple case of algebraic substitution and elimination: if $xy = x$ and $yz = y$, then by substituting $yz$ for $y$ in the first equation, and then using the first equation to eliminate $y$, we obtain $xz = x$.

The biggest difference, however, between Boole’s algebra and Boolean algebra as we know it today — and the one that caused most controversy at the time — is Boole’s definition of +. Boole defined addition partially, only on disjoint classes, i.e., $x + y$ is defined as the union of $x$ and $y$ only if $xy = 0$ (the ordinary, non-disjoint, union of two possibly intersecting classes could be written as $x(1-y) + y$). This means that in Boole’s algebra, the sum is not the dual of the product, and while multiplication distributes over addition, the converse does not hold as it does in modern Boolean algebra. Boole insisted on the disjoint union because he wanted his algebra to mimic the ordinary algebra as much as possible, and if $(x + y)^2 = x + y$ (by “Boole’s equation”, which states that for all $x$, $x^2 = x$), ordinary algebra would imply that $xy = 0$, so $x$ and $y$ must be disjoint.

This algebra of classes expresses what is known as term logic, which, in modern terms, corresponds to monadic first-order logic. But Boole notes that the same algebra has another interpretation, where the variables denote not classes but propositions. This interpretation corresponds to what we now call the propositional calculus. Note how Boole first says that instead of denoting a class of things, variables in the second interpretation denote the duration of time for which they are true, and so $xy$ would be the duration of time in which both X and Y are true. It is only because we usually talk about multiple propositions all applying to the same duration, which is usually always, that we just represent truth as 1 (although precisely it means “true for the entire duration of discourse”) and falsehood as 0:

⊕An Investigation of the Laws of Thought, p. 36-39 Every assertion that we make may be referred to one or the other of the two following kinds. Either it expresses a relation among things, or it expresses, or is equivalent to the expression of, a relation among propositions. An assertion respecting the properties of things, or the phænomena which they manifest, or the circumstances in which they are placed, is, properly speaking, the assertion of a relation among things. To say that “snow is white,” is for the ends of logic equivalent to saying, that “snow is a white thing.” An assertion respecting facts or events, their mutual connexion and dependence, is, for the same ends, generally equivalent to the assertion, that such and such propositions concerning those events have a certain relation to each other as respects their mutual truth or falsehood. The former class of propositions, relating to things, I call “Primary;” the latter class, relating to propositions, I call “Secondary.”

… For instance, the propositions, “The sun shines,” “The earth is warmed,” are primary; the proposition, “If the sun shines the earth is warmed,” is secondary. To say, “The sun shines,” is to say, “The sun is that which shines,” and it expresses a relation between two classes of things, viz., “the sun” and “things which shine” The secondary proposition, however, given above, expresses a relation of dependence between the two primary propositions, “The sun shines,” and “The earth is warmed.”

… If instead of the proposition, “The sun shines,” we say, “It is true that the sun shines,” we then speak not directly of things, but of a proposition concerning things… it is not of the things connected together in the primary proposition that any direct account is taken, but only of the proposition itself considered as true or as false.

In the expression both of primary and of secondary propositions, the same symbols, subject, as it will appear, to the same laws, will be employed in this work. The difference between the two cases is a difference not of form but of interpretation. In both cases the actual relation which it is the object of the proposition to express will be denoted by the sign =. In the expression of primary propositions, the members thus connected will usually represent the “terms” of a proposition, or, as they are more particularly designated, its subject and predicate.

⊕An Investigation of the Laws of Thought, p. 126-131 [I]n treating of secondary propositions, we find ourselves concerned with another class both of subjects and relations. For the subjects with which we have to do are themselves propositions, so that the question may be asked,–Can we regard these subjects also as things, and refer them, by analogy with the previous case, to a universe of their own? Again, the relations among these subject propositions are relations of coexistent truth or falsehood, not of substantive equivalence. We do not say, when expressing the connexion of two distinct propositions, that the one is the other, but use some such forms of speech as the following, according to the meaning which we desire to convey: “Either the proposition X is true, or the proposition Y is true;” “If the proposition X is true, the proposition Y is true;” “The propositions X and Y are jointly true;” and so on.

… Let x represent an act of the mind by which we fix our regard upon that portion of time for which the proposition X is true; and let this meaning be understood when it is asserted that x denotes the time for which the proposition X is true. Let us further employ the connecting signs +, -, =, &c., in the following sense, viz.: Let x + y denote the aggregate of those portions of time for which the propositions X and Y are respectively true, those times being entirely separated from each other. Similarly let x − y denote that remainder of time which is left when we take away from the portion of time for which X is true, that (by supposition) included portion for which Y is true.

… By continuing this method of reasoning it may be established, that the laws of combination of the symbols x, y, z, &c., in the species of interpretation here assigned to them, are identical in expression with the laws of combination of the same symbols, in the interpretation assigned to them in the first part of this treatise. The reason of this final identity is apparent. For in both cases it is the same faculty, or the same combination of faculties, of which we study the operations; operations, the essential character of which is unaffected, whether we suppose them to be engaged upon that universe of things in which all existence is contained, or upon that whole of time in which all events are realized, and to some part, at least, of which all assertions, truths, and propositions, refer.

Although the principles of expression which have been laid down are perfectly general, and enable us to limit our assertions of the truth or falsehood of propositions to any particular portions of that whole of time (whether it be an unlimited eternity, or a period whose beginning and whose end are definitely fixed, or the passing moment) which constitutes the universe of our discourse, yet, in the actual procedure of human reasoning, such limitation is not commonly employed. When we assert that a proposition is true, we generally mean that it is true throughout the whole duration of the time to which our discourse refers; and when different assertions of the unconditional truth or falsehood of propositions are jointly made as the premises of a logical demonstration, it is to the same universe of time that those assertions are referred, and not to particular and limited parts of it.

… We are here required to express that within those limits of time to which the matter of our discourse is confined the proposition X is true. Now the time for which the proposition X is true is denoted by x, and the extent of time to which our discourse refers is represented by 1. Hence we have

$x=1$

… We are here to express that within the limits of time to which our discourse relates, the proposition X is false; or that within those limits there is no portion of time for which it is true. Now the portion of time for which it is true is x. Hence the required equation will be

$x = 0$

In the concluding chapter of the book Boole writes:

⊕An Investigation of the Laws of Thought, pp. 319-320 It has been shown… that there is a scientific connexion between the conceptions of unity in Number, and the universe in Logic. They occupy in their respective systems the same relative place, and are subject to the same formal laws. Now to the Greek mind, in that early stage of activity,—a stage not less marked, perhaps not less necessary, in the progression of the human intellect, than the era of Bacon or of Newton,—when the great problems of Nature began to unfold themselves, while the means of observation were as yet wanting, and its necessity not understood, the terms “Universe” and “The One” seem to have been regarded as almost identical. To assign the nature of that unity of which all existence was thought to be a manifestation, was the first aim of philosophy. … The pantheistic tendency which pervaded many of these speculations is manifest in the language of Xenophanes, the founder of the Eleatic school, who, “surveying the expanse of heaven, declared that the One was God.” Perhaps there are few, if any, of the forms in which unity can be conceived, in the abstract as numerical or rational, in the concrete as a passive substance, or a central and living principle, of which we do not meet with applications in these ancient doctrines. … Strange, but suggestive truth, that while Nature in all but the aspect of the heavens must have appeared as little else than a scene of unexplained disorder, while the popular belief was distracted amid the multiplicity of its gods, —the conception of a primal unity, if only in a rude, material form, should have struck deepest root; surviving in many a thoughtful breast the chills of a lifelong disappointment, and an endless search!

⊕An Investigation of the Laws of Thought, pp. 323-324

⊕

… All sound philosophy gives its verdict against such speculations, if regarded as a means of determining the actual constitution of things. It may be that the progress of natural knowledge tends towards the recognition of some central Unity in Nature.

… If the study of the laws of thought avails us neither to determine the actual constitution of things, nor to explain the facts involved in that constitution which have perplexed the wise and saddened the thoughtful in all ages,— still less does it enable us to rise above the present conditions of our being, or lend its sanction to the doctrine which affirms the possibility of an intuitive knowledge of the infinite, and the unconditioned,—whether such knowledge be sought for in the realm of Nature, or above that realm. We can never be said to comprehend that which is represented to thought as the limit of an indefinite process of abstraction. A progression ad infinitum is impossible to finite powers. But though we cannot comprehend the infinite, there may be even scientific grounds for believing that human nature is constituted in some relation to the infinite. We cannot perfectly express the laws of thought, or establish in the most general sense the methods of which they form the basis, without at least the implication of elements which ordinary language expresses by the terms “Universe” and “Eternity.” As in the pure abstractions of Geometry, so in the domain of Logic it is seen, that the empire of Truth is, in a certain sense, larger than that of Imagination.

⊕An Investigation of the Laws of Thought, p. 327

… Perhaps the most obviously legitimate bearing of such speculations would be upon the question of the place of Mathematics in the system of human knowledge, and the nature and office of mathematical studies, as a means of intellectual discipline… Those who have maintained that the position of Mathematics is in both respects a fundamental one, have drawn one of their strongest arguments from the actual constitution of things. The material frame is subject in all its parts to the relations of number. All dynamical, chemical, electrical, thermal, actions, seem not only to be measurable in themselves, but to be connected with each other, even to the extent of mutual convertibility, by numerical relations of a perfectly definite kind. But the opinion in question seems to me to rest upon a deeper basis than this. The laws of thought, in all its processes of conception and of reasoning, in all those operations of which language is the expression or the instrument, are of the same kind as are the laws of the acknowledged processes of Mathematics. It is not contended that it is necessary for us to acquaint ourselves with those laws in order to think coherently, or, in the ordinary sense of the terms, to reason well. Men draw inferences without any consciousness of those elements upon which the entire procedure depends. Still less is it desired to exalt the reasoning faculty over the faculties of observation, of reflection, and of judgment. But upon the very ground that human thought, traced to its ultimate elements, reveals itself in mathematical forms, we have a presumption that the mathematical sciences occupy, by the constitution of our nature, a fundamental place in human knowledge, and that no system of mental culture can be complete or fundamental, which altogether neglects them.

But the very same class of considerations shows with equal force the error of those who regard the study of Mathematics, and of their applications, as a sufficient basis either of knowledge or of discipline. If the constitution of the material frame is mathematical, it is not merely so. If the mind, in its capacity of formal reasoning, obeys, whether consciously or unconsciously, mathematical laws, it claims through its other capacities of sentiment and action, through its perceptions of beauty and of moral fitness, through its deep springs of emotion and affection, to hold relation to a different order of things. There is, moreover, a breadth of intellectual vision, a power of sympathy with truth in all its forms and manifestations, which is not measured by the force and subtlety of the dialectic faculty.

Mary Everest Boole wrote:

⊕Indian Thought, pp. 5 At this point all possibility of becoming a priest came to an end. George set to work to write a book (The Laws of Thought), in order to give to the world his great discovery. If he had stated it in words, he would have been entangled in an unseemly theological skirmish. He presented the truth to the learned, clothed in a veil so transparent that it is difficult to conceive how any human being could have been blinded by it. … The academic world was enchanted. George visited Cambridge in 1855, a year after the publication, and was astonished, and at first gratified, at the cordiality of his reception. Herbert Spencer said that the book was “the greatest advance in Logic since Aristotle.” George Boole said to me that neither Aristotle’s Logic nor the Creed of Moses could have been enunciated unless the formula to which the Universities had now given the name of “Boole’s Equation” had been, in some form or other, perfectly well known. George afterwards learned, to his great joy, that the same conception of the basis of Logic was held by Leibnitz, the contemporary of Newton. De Morgan, of course, understood the formula in its true sense; he was Boole’s collaborator all along. Herbert Spencer, Jowett, and Leslie Ellis understood, I feel sure; and a few others, but nearly all the logicians and mathematicians ignored the statement that the book was meant to throw light on the nature of the human mind; and treated the formula entirely as a wonderful new method of reducing to logical order masses of evidence about external fact. Only think of it! The great English religious mind, which considers itself competent to preach the Truth, the only saving Truth, to all mankind; the great academic educational mind which is to improve Hindu culture off the face of the earth, fell into a trap which I believe would hardly have deceived a savage. My husband said to me that he believed he could never have made his discoveries if he had received a university education (as he at one time much wished to do, but was, fortunately, prevented by poverty). My after-experiences, among men who had been subjected to that process, incline me to think he was quite right in so believing. He was, as I said, a quiet student, gentle, timid, very conscientious, and averse to controversy; he could not face the theological animus which would be aroused by any attempt to explain himself in open words, nor did he feel it right to unsettle the superstitions of people evidently too stupid to take in reasonable truth; he went on to further researches.

He had proved the essential Tightness, in relation to human progress, of the command to think of the Infinite Unknown as Unity when appealing to Him for light on finite concerns.

Murawski writes that,Mechanization of Reasoning, Kindle Locations 2581-2586 “Boole’s works were rather ignored by most contemporary British logicians or damned with faint praise. One of persons who saw their importance was William Stanley Jevons (1835-1882), a logician and economist. He regarded Boole’s achievements as the greatest advance in the history of logic since Aristotle. But he noticed also defects of Boole’s system. He believed that it was a mistake that Boole tried to make his logical notation resemble algebraic notation. ‘I am quite convinced that Boole’s forms (…) have no real analogy to the similar mathematical expressions’ as he stated in a letter… He saw also the weakness in Boole’s preference for the exclusive rather than the inclusive interpretation of ‘or’.”

Boole’s use of an exclusive sum was a matter of intense debate between him and Jevons. Jevons objected to Boole’s adherence to the laws of ordinary algebra, and claimed that $x + x = x$ (whereas in Boole’s algebra, $x + x$ is undefined). Ultimately, Jevons won the debate, and in Boolean algebra the sum corresponds to an ordinary union. This would make the operations more suitable for expression as duals in an order theory, as we’ll see. Jevons then introduced his own new logical calculus, based on substitution, which I will not present here. He wrote:

⊕The Substitution of Similars, the True Principle of Reasoning, pp. 5-9 When Hobbes, in the time of the Commonwealth, published his ‘Computation or Logique,’ he had a remote glimpse of some of the points which are placed in the light of day by Mr. Boole.

… The quasi-mathematical methods of Dr. Boole especially are so mystical and abstruse, that they appear to pass beyond the comprehension and criticism of most other writers, and are calmly ignored.

… The proposition becomes an equation of subject and predicate, and the significance of this change will be fully apparent only to those who see that logical science thus acquires a point of contact with mathematical science. Nor is it only in a single point that the two great abstract sciences meet. Dr. Boole’s remarkable investigations prove that, when once we view the proposition as an equation, all the deductions of the ancient doctrine of logic, and many more, may be arrived at by the processes of algebra. Logic is found to resemble a calculus in which there are only two numbers, 0 and 1, and the analogy of the calculus of quality or fact and the calculus of quantity proves to be perfect. Here, in all probability, we shall meet a new instance of the truth observed by Baden Powell, that all the greatest advances in science have arisen from combining branches of science hitherto distinct, and in showing the unity of principles pervading them…

And yet anyone acquainted with the systems of the modern logicians must feel that something is still wanting. So much diversity and obscurity are no usual marks of truth, and it is almost incredible that the true general system of inference should be beyond the comprehension of nearly every one, and therefore incapable of affecting ordinary thinkers. I am thus led to believe that the true clue to the analogy of mathematics and logic has not hitherto been seized.

The Mind’s Rival in the Wheels and Levers of an Insensible Machine

Unlike Boole, Jevons explicitly discussed the construction of calculating machines (and even created one of his own, designed to assist in logical operations) and how Boole’s achievement suggests that an “an all-embracing system” of mechanical reasoning is possible, by which the mind will “create its own rival”. He writes:

⊕On the Mechanical Performance of Logical Inference, 1869 ⊕
Jevons’s logical piano blueprint, from On the Mechanical Performance of Logical InferenceIt is an interesting subject for reflection that from the earliest times mechanical assistance has been required in mental operations. The word calculation at once reminds us of the employment of pebbles for marking units, and it is asserted that the word ἀριθμὸϛ is also derived from the like notion of a pebble or material sign. Even in the time of Aristotle the wide extension of the decimal system of numeration had been remarked and referred to the use of the fingers in reckoning; and there can be no doubt that the form of the most available arithmetical instrument, the human hand, has reacted upon the mind and moulded our numerical system into a form which we should not otherwise have selected as the best.

… It was reserved for the profound genius of Mr. Babbage to make the greatest advance in mechanical calculation, by embodying in a machine the principles of the calculus of differences. Automatic machinery thus became capable of computing the most complicated mathematical tables; and in his subsequent design for an Analytical Engine Mr. Babbage has shown that material machinery is capable, in theory at least, of rivalling the labours of the most practised mathematicians in all branches of their science. Mind thus seems able to impress some of its highest attributes upon matter, and to create its own rival in the wheels and levers of an insensible machine.

It is highly remarkable that when we turn to the kindred science of logic we meet with no real mechanical aids or devices. Logical works abound, it is true, with metaphorical expressions implying a consciousness that our reasoning powers require such assistance, even in the most abstract operations of thought. In or before the 15th century the logical works of the greatest logician came to be commonly known as the Organon or Instrument, and, for several centuries, logic itself was defined as Ars instrumentalis dirigens mentem nostram in cognitionem omnium intelligibilium.The instrumental technique for directing our mind to the knowledge of all that is intelligible

When Francis Bacon exposed the futility of the ancient deductive logic, he still held that the mind is helpless without some mechanical rule, and in the second aphorism of his ‘New Instrument ‘ he thus strikingly asserts the need :—

Nee manus nuda, nee Intellects sibi permissus, multum valet ; Instrumentis et auxiliis res perficitur; quibus opus est, non minus ad intellectum, quam ad manum. Atque ut instrumenta manus motum ant cient, aut regunt ; ita et Instrumenta mentis, Intellectui aut suggerunt aut cavent.Neither the the hand nor the intellect do much on their own; the work is no less that of the intellect than of the hand. And as the mind guides the motion of the hand, the hand protects the understsanding of the mind

⊕
Jevons’s logical piano, built in Machester in 1869 and displayed at the Museum of the History of Science, Oxford. A Dvorak version was also available.

In all such expressions, however, the word Instrument is used metaphorically to denote an invariable formula or rule of words, or system of procedure. Even when Raymond Lully put forth his futile scheme of a mechanical syllogistic, the mechanical apparatus consisted of nothing but written diagrams. It is rarely indeed that any invention is made without some anticipation being sooner or later discovered; but up to the present time I am totally unaware of even a single previous attempt to devise or construct a machine which should perform the operations of logical inference; and it is only I believe in the satirical writings of Swift that an allusion to an actual reasoning machine is to be found.

The only reason which I can assign for this complete inability of logicians to devise a real logical instrument, is the great imperfection of the doctrines which they entertained. Until the present century logic has remained substantially as it was moulded by Aristotle 2200 years ago… And I venture to look upon the logical machine which I am about to describe as equally a result and indication of a profound reform and extension of logical science accomplished within the present century by a series of English writers…

To George Boole, even more than to any of the logicians I have named, this great advance in logical doctrine is due. … [H]e first put forth the problem of logical science in its complete generality :— Given certain logical premises or conditions, to determine the description of any class of objects under those conditions. Such was the general problem of which the ancient logic had solved but a few isolated cases—the nineteen moods of the syllogism, the sorites, the dilemma, the disjunctive syllogism, and a few other forms. Boole showed incontestably that it was possible, by the aid of a system of mathematical signs, to deduce the conclusions of all these ancient modes of reasoning, and an indefinite number of other conclusions. Any conclusion, in short, that it was possible to deduce from any set of premises or conditions, however numerous and complicated, could be calculated by his method.

Yet Boole’s achievement was rather to point out the extent of the problem and the possibility of solving it, than himself to give a clear and final solution. As readers of his logical works must be well aware, he shrouded the simplest logical processes in the mysterious operations of a mathematical calculus.

… Having made Boole’s logical works a subject of study for many years past, I endeavoured to show in my work on Pure Logic that the mysterious mathematical forms of Boole’s logic are altogether superfluous, and that in one point of great importance, the employment of exclusive instead of unexclusive alternatives, he was deeply mistaken. Rejecting the mathematical dress and the erroneous conditions of his symbols, we arrive at a logical method of the utmost generality and simplicity… The logical machine which I am about to describe is no mere model illustrative of the fixed forms of the syllogism. It is an analytical engine of a very simple character, which performs a complete analysis of any logical problem impressed upon it.

… I may add a few words to deprecate the notion that I attribute much practical utility to this mechanical device… The chief importance of the machine is of a purely theoretical kind. It demonstrates in a convincing manner the existence of an all-embracing system of Indirect Inference, the very existence of which was hardly suspected before the appearance of Boole’s logical works.

John Venn (1834 – 1923) commented on the use of the word “algorithm” to describe logic, and also on the difference between Leibniz’s work and Boole’s:

⊕Symbolic Logic, pp. 98-99 It is to this generalized symbolic language, such as we are here employing it, that some writers have applied, by a revival of an old word, the term Algorithm. Thus, for example, Delbœuf entitles his work, written on the same kind of subject as this, “Logique algorithmique.” There is no objection whatever to the word, but I have preferred to speak of “Symbolic Logic” as being more familiar in our language : ‘symbolic’ as I understand it, being almost exactly the equivalent of ‘algorithmic.’

⊕
A Venn diagram, from On the Diagrammatic and Mechanical Representation of Propositions and Reasonings. Not quite the same thing as an Euler diagram (see The Algebra of Thought).

There is also another old term which will be familiar to readers of Leibnitz and Wolf,—characteristic,—which seems to me to cover much the same ground as Algorithmic and Symbolic… but the discussions on this subject are much mixed up with the wider question of a general philosophical language. As the reader very likely knows, this problem was keenly discussed in the seventeenth and eighteenth centuries and occupied the attention of Leibnitz more or less throughout his life. Speaking from a very slight acquaintance, I should say that what was mostly contemplated by the writers in question was more what we should now call either a universal language, or a general system of shorthand, than a logic. I mean that they do not attempt any analysis of the reasoning processes; and that the words or symbols proposed by them do not stand perfectly generally for any classes whatever, like our x and y, but specially for such and such well-known classes as are already designated by general names; they differ, in fact, as language does and should differ from logic.

Venn, however, was skeptical of the utility of logical machines:

⊕On the Diagrammatic and Mechanical Representation of Propositions and Reasonings, pp. 15-16 ⊕
A Venn machine, from On the Diagrammatic and Mechanical Representation of Propositions and Reasonings. Despite his skepticism, ‘corresponding to Prof. Jevons’s logical machine’, Venn describes his own ‘contrivance’: ‘I prefer to call it merely a logical-diagram machine, for the reasons already given; but I suppose that it would do very completely all that can be rationally expected of any logical machine. Certainly, as regards portability, nothing has been proposed to equal it, so far as I know; for though needlessly large as made by me, it is only between five and six inches square and three inches deep’.It will be easily seen that such methods as those here described readily lend themselves to mechanical performance. I have no high estimate myself of the interest or importance of what are sometimes called logical machines, and this on two grounds. In the first place, it is very seldom that intricate logical calculations are practically forced upon us ; it is rather we who look about for complicated examples in order to illustrate our rules and methods. In this respect logical calculations stand in marked contrast with those of mathematics, where economical devices of any kind may subserve a really valuable purpose by enabling us to avoid otherwise inevitable labour. Moreover, in the second place, it does not seem to me that any contrivances at present known or likely to be discovered really deserve the name of logical machines. It is but a very small part of the entire process which goes to form a piece of reasoning which they are capable of performing. For, if we begin from the beginning, that process would involve four tolerably distinct steps. There is, first, the statement of our data in accurate logical language. This step deserves to be reckoned, since the variations of popular language are so multitudinous, and often so vague and ambiguous, that they may need careful consideration before they can be reduced to form. Then, secondly, we have to throw these statements into a form fit for the engine to work with–in this case the reduction of each proposition to its elementary denials. It would task the energies of a machine to deal at once, say, with all the premises employed even in the few examples here offered. Thirdly, there is the combination or further treatment of our premises after such reduction. Finally, the results have to be interpreted or read off. This last generally gives rise to much opening for skill and sagacity ; for though in such examples as the last … there is but one answer fairly before us, yet in most cases there are many ways of reading off the answer. It then becomes a question of judgment which of these is the simplest and best. For instance, in the last example but one, there are a quantity of alternative ways of reading off our conclusion ; and until this is done the problem cannot be said to be solved. I cannot see that any machine can hope to help us except in the third of these steps ; so that it seems very doubtful whether any thing of this sort really deserves the name of a logical engine.

Yet another who elaborated on Boole’s work was the American philosopher Charles Sanders Peirce (1839-1914), father of the philosophical tradition of pragmatism. In a seminal 1880 paper that gave birth to lattice theorySee Štěpánka Bilová, Lattice Theory, its Birth and Life, 1999 he summarizes his work (and compares it to similar work done contemporaneously by Ernst Schröder and Robert Grassman) on a logical algebra building upon Boole’s, where an order relation, subsumption (or implication) — written as the symbol $-\!\!\!<$ — is used instead of equality, and the sum and the product are defined, dually, as the supremum and the infimum. He uses Boole’s 0 as representing the empty class, but the universe, instead of 1, is designated by ∞. This was the beginning of order theory.

He lays the definitions of addition and multiplication side by side (as he writes Schröder had done) to show their duality:These very definitions would be generalized in the 20th century as the universal constructions of the product and sum/coproduct in category theory.

⊕On the Algebra of Logic, p. 33

If $a -\!\!\!< x$ and $b -\!\!\!< x$,		If $x -\!\!\!< a$ and $x -\!\!\!< b$,
then $a + b -\!\!\!< x$;		then $x -\!\!\!< a \times b$;
and conversely,		and conversely,
if $a + b -\!\!\!< x$,		if $x -\!\!\!< a \times b$
then $a -\!\!\!< x$ and $b -\!\!\!< x$.		then $x -\!\!\!< a$ and $x -\!\!\!< b$.

Peirce adopted Jevon’s, rather than Boole’s, definition of addition (or disjunction) as a union rather than a disjoint union, because it presented the operations of multiplication (conjunction) and addition (disjunction) as duals of each other, or, as Peirce called it, being in “perfect balance”:

⊕On the Algerba of Logic, p. 32 I regret that I can only speak of this work from having read it many years ago, and therefore cannot be sure of doing it full justice – improved the algebra of Boole by substituting De Morgan’s aggregation for Boole’s addition. The present writer, not having seen either De Morgan’s or Jevons’s writings on the subject, again recommended the same change… and showed the perfect balance existing between the two operations.

Like Leibniz and Boole, Peirce also seeks to establish logical algebra on the reality of human cognition. Recent discoveries about the brain in the 1860s and ’70s allowed Peirce to tie algebraic logic to the very structure and function of the nerve cells. That seminal paper in algebra and order theory begins thus:

⊕On the Algerba of Logic, pp. 15-17 In order to gain a clear understanding of the origin of the various signs used in logical algebra and the reasons of the fundamental formulæ, we ought to begin by considering how logic itself arises.

Thinking, as cerebration, is no doubt subject to the general laws of nervous action.

When a group of nerves are stimulated, the ganglions with which the group is most intimately connected on the whole are thrown into an active state, which in turn usually occasions movements of the body. The stimulation continuing, the irritation spreads from ganglion to ganglion (usually increasing meantime). Soon, too, the parts first excited begin to show fatigue; and thus for a double reason the bodily activity is of a changing kind. When the stimutlus is withdrawn, the excitement quickly subsides.

… Accordingly, when an irritation of the nerves is repeated, all the various actions which have taken place on previous similar occasions are the more likely to take place now, and those are most likely to take place which hiave most frequently taken place on those previous occasions. … Hence, a strong, habit of responding to the given irritation in this particular way must quickly be established.

A habit so acquired may be transmitted by inheritance.

Very often it is not an outward sensation but only a fancy which starts the train of thought. In other words, the irritation instead of being peripheral is visceral. In such a case the activity has for the most part the same character… A fancied conjuncture leads us to fancy an appropriate line of action. It is found that such events, though no external action takes place, strongly contribute to the formation of habits of really acting in the fancied way when the fancied occasion really arises.

A cerebral habit of the highest kind, which will determine what we do in fancy as well as what we do in action, is called a belief. The representation to ourselves that we have a specified habit of this kind is called a judgment. A belief-habit in its development begins by being vague, special, and meagre; it becomes more precise, general, and full, without limit. The process of this development, so far as it takes place in the imagination, is called thought. A judgment is formed; and under the influence of a belief-habit this gives rise to a new judgment, indicating, an addition to belief. Such a process is called an inference; the antecedent judgment is called the premise; the consequent judgment, the conclusion…

At the same time that this process of inference, or the spontaneous development of belief, is continually going on within us, fresh peripheral excitations are also continually creating new belief-habits. Thus, belief is partly determined by old beliefs and partly by new experience. Is there any law about the mode of the peripheral excitations? The logician maintains that there is, namely, that they are all adapted to an end, that of carrying belief, in the long run, toward certain predestinate conclusions which are the same for all men. This is the faith of the logician. This is the matter of fact, upon which all maxims of reasoning repose. In virtue of this fact, what is to be believed at last is independent of what has been believed hitherto, and therefore has the character of reality. Hence, if a given habit, considered as determining an inference, is of such a sort as to tend toward the final result, it is correct; otherwise not. Thus, inferences become divisible into the valid and the invalid; and thus logic takes its reason of existence.

… The passage from the premise (or set of premises) P to the conclusion C takes place according to a habit or rule active within us. All the inferences which that habit would determine when once the proper premises were admitted, form a class. The habit is logically good provided it wouild never (or in the case of a probable inference, seldom) lead from a true premise to a false conclusion.

…

⊕Footnote, p.21 In logic, our great object is to analyze all the operations of reason and reduce them to their ultimate elements; and to make a calculus of reasoning is a subsidiary object.

Despite this appeal to biology, Peirce establishes his algebra on Aristotelian logic, presenting a formalization of the old Aristotelian syllogisms in his new system. Like Venn, Peirce saw a connection between the algebra of logic and computing machines, although he was much more optimistic of their potential than Venn:

⊕Logical Machines, 1887 ⊕
Lemuel Gulliver discovers the flying island of Laputa, home of curious, though comically impractical, intellectuals. Illustration by Thomas Morten (1836-1866) to Jonathan’s Swift’s Gulliver’s Travels, 1726 (source) In the “Voyage to Laputa” there is a description of a machine for evolving science automatically. “By this contrivance, the most ignorant person, at a reasonable charge, and with little bodily labor, might write books in philosophy, poetry, politics, laws, mathematics, and theology, without the least assistance from genius or study.” The intention is to ridicule the Organon of Aristotle and the Organon of Bacon, by showing the absurdity of supposing that any “instrument” can do the work of the mind. Yet the logical machines of Jevons and Marquand are mills into which the premises are fed and which turn out the conclusions by the revolution of a crank. The numerous mathematical engines that have been found practically useful, from Webb’s adder up to Babbage’s analytical engine (which was designed though never constructed), are also machines that perform reasoning of no simple kind. Precisely how much of the business of thinking a machine could possibly be made to perform, and what part of it must be left for the living mind, is a question not without conceivable practical importance; the study of it can at any rate not fail to throw needed light on the nature of the reasoning process. Though the instruments of Jevons and of Marquand were designed chiefly to illustrate more elementary points, their utility lies mainly, as it seems to me, in the evidence they afford concerning this problem.

⊕
Allan Marquand’s (1853–1924) logical machine (source).

… Every reasoning machine, that is to say, every machine, has two inherent impotencies. In the first place, it is destitute of all originality, of all initiative. It cannot find its own problems; it cannot feed itself. It cannot direct itself between different possible procedures. For example, the simplest proposition of projective geometry, about the ten straight lines in a plane, is proved by von Staudt from a few premises and by reasoning of extreme simplicity, but so complicated is the mode of compounding these premises and forms of inference, that there are no less than 70 or 80 steps in the demonstration. How could we make a machine which would automatically thread its way through such a labyrinth as that? And even if we did succeed in doing so, it would still remain true that the machine would be utterly devoid of original initiative, and would only do the special kind of thing it had been calculated to do. This, however, is no defect in a machine; we do not want it to do its own business, but ours. The difficulty with the balloon, for instance, is that it has too much initiative, that it is not mechanical enough. We no more want an original machine, than a house-builder would want an original journeyman, or an American board of college trustees would hire an original professor. If, however, we will not surrender to the machine, the whole business of initiative is still thrown upon the mind; and this is the principal labor.

⊕
A circuit diagram for Marquand’s electromagnetic logical machine, 1890. The use of electricity was suggested by Peirce, who may have designed the whole mechanism. (source)

In the second place, the capacity of a machine has absolutely limitations; it has been contrived to do a certain thing, and it can do nothing else. For instance, the logical machines that have thus far been devised can deal with but a limited number of different letters. The unaided mind is also limited in this as in other respects; but the mind working with a pencil and plenty of paper has no such limitation. It presses on and on, and whatever limits can be assigned to its capacity to-day, may be over-stepped to-morrow. This is what makes algebra the best of all instruments of thought; nothing is too complicated for it. And this great power it owes, above all, to one kind of symbol, the importance of which is frequently entirely overlooked—I mean the parenthesis. We can, of course, dispense with the parentheses as such. Instead of $(a + b)c = d$, we can write $a + b = t$ and $tc = d$. The letter $t$ is here a transmogrified parenthesis. We see that the power of adding proposition to proposition is in some sort equivalent to the use of a parenthesis.

It is fascinating that Peirce points out the limitation of the unaided mind, and how that limitation can be removed with the aid of “a pencil and plenty of paper”, an observation made by Leibniz, and which later formed the basis of Turing’s analysis of computation. Also of interest is his observation that parentheses — and, more importantly, their implied use in the process of substitution — which is at the heart of the power of algebra.

The algebraic school in logic of the 19th century, begun by Boole, wholly endorsed, perhaps unknowingly, Leibniz’s view that logic is the formulation of the mind, whose process is computation (although Lovelace rejected that belief, and Peirce saw a reasonable division of labor between the work of the mind and that of the machine), and algebra is its mathematical expression. They fully and explicitly embraced the unity of algebra or symbolic manipulation with the concept of the algorithm, as is apparent in Venn’s and Peirce’s texts. The founders of abstract algebra were the logicians of the nineteenth century and the designers of computing machines — the proto-computers.

This unified, or shall I say — in the spirit of George Boole’s religious philosophy — monistic, view began to crack in 1879 with the works of Gottlob Frege. But as Frege’s work was originally rejected precisely for abandoning this unity and was only accepted in the twentieth century, after serving as the starting point for Bertrand Russell and Alfred North Whitehead’s Principa Mathematica, I shall postpone discussing it to the next part, that concerns the developments in logic and computation in the twentieth century.

Furthermore, while Boole’s algebra is certainly an algebra of logic, the fact that it was not quite right and not only had to be adapted — by Jevons, Peirce, Schröder and others — to better accommodate logic, shows that, at least in this case, the correspondence between logic and algebra was not discovered but very much invented. In fact, the very notion of algebra had to be modified in order to create this more perfect union. This algebra of logic was later generalized — first by Heyting algebras (also called pseudo-Boolean algebras), which drop the requirement for the existence of a complement, and then by certain categories in category theory (where a Cartesian-closed poset, i.e., a category restricted to at most one morphism in every hom-set, is a Heyting algebra) — and it is not surprising that those generalizations beautifully correspond with logic; it would have been truly surprising if they failed at that task.

Finally, despite Boole’s claims that he studied the human mind and Peirce’s anchoring of algebra on biological nature of the brain as he believed it to be, it was the Aristotelian formulation of human thought that they took on faith. The logical algebra that the nineteenth century mathematicians/logicians designed was not an algebra of any arbitrary logic, and certainly not a universal mathematical tool for the analysis of human reasoning, but rather a mathematical model of a very particular logic, describing a very particular — and ancient — view of human thought.

Part 1, Part 3